20 câu Trắc nghiệm Toán 10 Chân trời sáng tạo Bài 2. Định lí côsin và định lí sin (Đúng-sai, trả lời ngắn) có đáp án
20 câu hỏi
Cho \[\Delta ABC\] có \[AB = 5\]; \(\widehat A = 40^\circ \); \(\widehat B = 60^\circ \). Độ dài \[BC\] gần nhất với kết quả nào?
\[3,7\].
\[3,3\].
\[3,5\].
\[3,1\].
Cho tam giác \(ABC\) có \(AB = 4\)cm, \(BC = 7\)cm, \(AC = 9\)cm. Tính \(\cos A\).
\(\cos A = - \frac{2}{3}\).
\(\cos A = \frac{1}{2}\).
\(\cos A = \frac{1}{3}\).
\(\cos A = \frac{2}{3}\).
Cho \(\Delta ABC\) có góc \(\widehat {BAC} = 60^\circ \) và cạnh \(BC = \sqrt 3 \). Tính bán kính của đường tròn ngoại tiếp \(\Delta ABC\).
\(R = 4\).
\(R = 1\).
\(R = 2\).
\(R = 3\).
Cho \(\Delta ABC\) với các cạnh \(AB = c,\,\,AC = b,\,\,BC = a\). Gọi \(R,\,\,r,\,\,S\) lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và diện tích của tam giác \(ABC\). Công thức nào sau đây sai?
\[S = \frac{1}{2}ab\sin A\].
\(S = \frac{1}{2}ab\sin C\).
\[S = \frac{{abc}}{{4R}}\].
\[S = \frac{{\left( {a + b + c} \right)r}}{2}\].
Cho tam giác ABC có \(a = 8,b = 10\), góc \(C\) bằng \(60^\circ \). Độ dài cạnh \(c\) là:
\(c = 3\sqrt {21} \).
\(c = 7\sqrt 2 \).
\(c = 2\sqrt {11} \).
\(c = 2\sqrt {21} \).
Cho tam giác \(ABC\) có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác \(ABC\) bằng
\(12\).
\(3\).
\(6\).
\(24\).
Một tam giác có ba cạnh là \(13,14,15\). Diện tích tam giác đó bằng
\(84\,.\)
\[\sqrt {84} \,.\]
\(42\,.\)
\[\sqrt {168} \,.\]
Cho tam giác \(ABC\), biết \(a = 13,b = 14,c = 15.\) Tính góc \(B\).
\(59^\circ 49'.\)
\(53^\circ 7'.\)
\(59^\circ 29'\,.\)
\(62^\circ 22'.\)
Tam giác \[ABC\] có \(\widehat B = 45^\circ ,\widehat C = 60^\circ \), \[b = 2\]. Tính cạnh \[c\].
\(\frac{{\sqrt 2 }}{2}\).
\(\frac{{\sqrt 6 }}{3}\).
\(\frac{{\sqrt 6 }}{2}\).
\(\sqrt 6 \).
Cho tam giác \(ABC\) có \(AB = 2a;\,\,AC = 4a\) và \(\widehat {BAC} = 120^\circ \). Diện tích tam giác \(ABC\) là:
\(S = 8{a^2}\).
\(S = 4{a^2}\).
\(S = {a^2}\sqrt 3 \).
\(S = 2{a^2}\sqrt 3 \).
Cho tam giác \(ABC\) có \(b = 7\;\,{\rm{cm}},c = 5\;\,{\rm{cm}},\widehat A = 120^\circ \).
a) \(a = \sqrt {127} \;\,{\rm{cm}}\).
b) \(\cos B \approx 0,21\).
c) \(\cos C \approx 0,91\).
d) \(R \approx 6,03\,{\rm{cm}}\).
Cho tam giác \(ABC\) có số đo các cạnh lần lượt là \(7,9\) và \(12\). Gọi \(S,R,p,r\) lần lượt là diện tích, bán kính đường tròn ngoại tiếp, nửa chu vi, bán kính đường tròn nội tiếp tam giác.
a) \(p = 14\).
b) \(S = 13\sqrt 5 \).
c) \(R = \frac{{7\sqrt 5 }}{{10}}\).
d) \(r = \sqrt 3 \).
Cho \(\Delta ABC\) có \(BC = \sqrt 6 ,CA = 2,AB = 1 + \sqrt 3 \).
a) \(\widehat A = 30^\circ \).
b) \(\widehat B = 35^\circ \).
c) Diện tích của \(\Delta ABC\) là \(S = \frac{{3 + \sqrt 3 }}{2}\).
d) Bán kính đường tròn ngoại tiếp \(\Delta ABC\) là \(R = \sqrt 2 .\)
Cho tam giác \[ABC\] có \[BC = a = 8,AB = c = 5,\widehat {ABC} = 60^\circ \].
a) Độ dài cạnh \[AC = 7\].
b) \[\widehat {BAC}\] là góc tù.
c) Bán kính đường tròn ngoại tiếp tam giác \[ABC\] bằng \(\frac{{7\sqrt 3 }}{3}\).
d) Biểu thức \[T = \sin A - 2\sin B + \sin C\] có giá trị bằng 0.
Cho tam giác \(ABC\), biết \(AC = b = 7,AB = c = 5,\cos A = \frac{3}{5}\).
a) \(\sin A = \frac{4}{5}\).
b) Diện tích tam giác \(ABC\) là \(S = 14\).
c) Độ dài cạnh BC là \(a = 3\sqrt 2 \).
d) Bán kính đường tròn nội tiếp tam giác \(ABC\) là \(r = 4 - \sqrt 2 \).
Cho \(\Delta ABC\) có \(AB = 8,AC = 5,\widehat {BAC} = 60^\circ \). Tính chiều cao \(AH\) của \(\Delta ABC\) (kết quả làm tròn đến hàng phần trăm).
Cho tam giác \(ABC\) có \(\frac{5}{{\sin A}} = \frac{4}{{\sin B}} = \frac{3}{{\sin C}}\) và \(a = 10\). Tính chu vi tam giác đó.
Cho tam giác \(ABC\) có \(BC = a,CA = b,AB = c\) biết \(a \ne b\) và \(a\left( {{a^2} - {c^2}} \right) = b\left( {{b^2} - {c^2}} \right)\). Khi đó, số đo của \(\widehat {{\mkern 1mu} C{\mkern 1mu} }\) bằng bao nhiêu độ?
Tam giác \(ABC\) có góc \(A\) nhọn, \(AB = 5\), \(AC = 8\), diện tích bằng \(12\). Tính độ dài cạnh \(BC\).
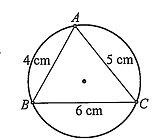
Từ một miếng bìa hình tròn, bạn Nam cắt ra một hình tam giác \(ABC\) có độ dài các cạnh \(AB = 4\;{\rm{cm}},AC = 5\;{\rm{cm}},BC = 6\;{\rm{cm}}\) (Hình vẽ). Tính bán kính \(R\) của miếng bìa ban đầu (làm tròn kết quả đến hàng đơn vị theo đơn vị centimét).