20 câu Trắc nghiệm Toán 10 Cánh diều Bài 5. Hai dạng phương trình quy về phương trình bậc hai (Đúng-sai, trả lời ngắn) có đáp án
20 câu hỏi
Số nào dưới đây là nghiệm của phương trình \(\sqrt {2{x^2} + x + 3} = \sqrt {{x^2} + 2x + 5} \)?
\(x = 2.\)
\(x = - 3.\)
\(x = - 2.\)
\(x = 1.\)
Số nghiệm của phương trình \(\sqrt {{x^2} - 4x - 7} = \sqrt { - {x^2} + 6x - 7} \) là
\(2\).
\(1\).
\(0\).
\(3\).
Số nghiệm của phương trình \[\sqrt {3{x^2} - 4x - 1} = \sqrt {2{x^2} - 4x + 3} \] là:
2.
3.
0.
1.
Tập nghiệm của phương trình \[\sqrt {{x^2} - 2x - 4} = \sqrt {2 - x} \] là
\[\left\{ {3; - 2} \right\}\].
\[\left\{ 3 \right\}\].
\[\left\{ { - 2} \right\}\].
\[\left\{ {3;2} \right\}\].
Phương trình \(\sqrt { - {x^2} + 4x} = 2x - 2\) có nghiệm là
\(x = \frac{2}{5};\,x = 2\).
\(x \in \emptyset \).
\(x = 2\).
\(x = 1\).
Số nghiệm của phương trình \(\sqrt {4 - 3{x^2}} = 2x - 1\) là:
\(0.\)
\(1.\)
\(2.\)
\(3.\)
Số nghiệm của phương trình sau \[x - \sqrt {2{x^2} - 3x + 1} = 1\] là:
\(0\).
\(1\).
\(2\).
\(3\).
Tập nghiệm của phương trình \(\sqrt {2{x^2} + 4x - 1} = x + 1\) là
\(S = \left\{ { - 1 + \sqrt 3 ; - 1 - \sqrt 3 } \right\}.\)
\(S = \left\{ { - 1 + \sqrt 3 } \right\}.\)
\(S = \left\{ { - 1 - \sqrt 3 } \right\}.\)
\(S = \emptyset .\)
Phương trình \(\sqrt {{x^2} + x + 1} = \sqrt {x + 2} \) có tập nghiệm là
\(\left\{ { - 3;1} \right\}\).
\(\left\{ { - 1;1} \right\}\).
\(\left\{ {0;1} \right\}\).
\(\left\{ { - 1} \right\}\).
Phương trình \(\sqrt {2{x^2} + 3x - 5} = x + 1\) có nghiệm là
\(x = 4\).
\(x = 3\).
\(x = 1\).
\(x = 2\).
Cho phương trình \(\sqrt {5{x^2} - 8x + 2} = \sqrt {{x^2} + 2} \) (*).
a) \({x^2} + 2 > 0\) đúng \(\forall x \in \mathbb{R}\).
b) Bình phương hai vế của phương trình (*) ta được \(4{x^2} - 3x = 0\).
c) Phương trình (*) có 2 nghiệm.
d) Tổng các nghiệm của phương trình (*) bằng 0.
Cho phương trình \(\sqrt {2{x^2} + x - 6} = x + 2\) (*).
a) Bình phương hai vế phương trình (*) ta được \({x^2} - 3x - 10 = 0\).
b) Điều kiện của phương trình (*) là \(x \ge 2\).
c) Phương trình (*) có 2 nghiệm.
d) Tích các nghiệm của phương trình (*) bằng 10.
Cho phương trình \(\sqrt {{x^2} + 2x + 4} = \sqrt {2 - x} \) (*).
a) Điều kiện của phương trình là \(x \le 2\).
b) Bình phương hai vế của phương trình (*) ta được \({x^2} + 3x + 1 = 0\).
c) Phương trình (*) có 2 nghiệm phân biệt.
d) Các nghiệm của phương trình (*) thuộc \(\mathbb{Z}\).
\ (\ sqrt {{x^2} + 2x + 4} = \ sqrt {2 - x} \) (*).
Cho phương trình \(\sqrt {2{x^2} + 5} = \sqrt {{x^2} - x + 11} \) (*).
a) Điều kiện: \(x \ge 0\).
b) Bình phương hai vế của phương trình (*) ta được \({x^2} + x - 6 = 0\).
c) Phương trình (*) có 1 nghiệm.
d) Giả sử \({x_1},{x_2}\,\left( {{x_1} < {x_2}} \right)\) là nghiệm của phương trình (*) khi đó: \({x_1} - 2{x_2} = 7\).
Cho phương trình \(\left( {x - 2} \right)\sqrt {2{x^2} + 4} = {x^2} - 4\).
a) \(x = 2\) là một nghiệm của phương trình đã cho.
b) Phương trình đã cho có 3 nghiệm phân biệt.
c) Tổng các nghiệm của phương trình đã cho bằng 5.
d) Các nghiệm của phương trình đã cho là các số chẵn.
\ (\ left ({x - 2} \ right) \ sqrt {2 {x^2} + 4} = {x^2} - 4 \).
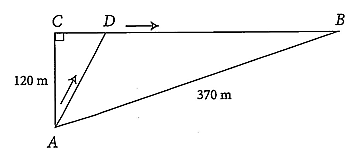
Một chú thỏ ngày nào cũng ra bờ suối ở vị trí \(A\), cách cửa hang của mình tại vị trí \(B\) là \(370{\rm{\;m}}\) để uống nước, sau đó chú thỏ sẽ đến vị trí \(C\) cách vị trí \(A\) một khoảng \(120\;{\rm{m}}\) để ăn cỏ rồi trở về hang. Tuy nhiên, hôm nay sau khi uống nước ở bờ suối, chú thỏ không đến vị trí \(C\) như mọi ngày mà chạy đến vị trí \(D\) để tìm cà rốt rồi mới trở về hang (xem hình bên dưới). Biết rằng, tổng thời gian chú thỏ chạy từ vị trí \(A\) đến vị trí \(D\) rồi về hang là 30 giây (không kể thời gian tìm cà rốt), trên đoạn \(AD\) chú thỏ chạy với vận tốc là \(13\;\,{\rm{m/s}}\), trên đoạn \(BD\) chú thỏ chạy với vận tốc là \(15\;\,{\rm{m/s}}\). Tính khoảng cách giữa hai vị trí \(C\) và \(D\) (đơn vị: mét).
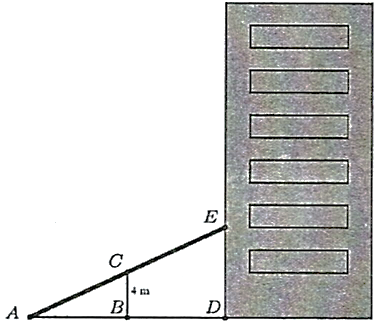
Người ta làm ra một cái thang bắc lên tầng hai của một ngôi nhà (hình vẽ), muốn vậy họ cần làm một thanh đỡ \(BC\) có chiều dài bằng \(4\;{\rm{m}}\), đồng thời muốn đảm bảo kỹ thuật thì tỉ số độ dài \(\frac{{CE}}{{BD}} = \frac{5}{3}\). Hỏi vị trí \(A\) cách vị trí \(B\) bao nhiêu mét?
Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {{x^2} + 2x - m} = 2x - 1\) có 2 nghiệm thực phân biệt.
Một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển một khoảng cách \(AB = 6\;{\rm{km}}\). Trên bờ biển có một cái kho ở vị trí \(C\) cách \(B\) một khoảng là \(15\;{\rm{km}}\).
Để nhận lương thực và các nhu yếu phẩm mỗi tháng người canh hải đăng phải đi xuống máy từ \(A\) đến bến tàu \(M\) trên bờ biển với vận tốc \(10\;{\rm{km/h}}\) rồi đi xe gắn máy đến \(C\) với vận tốc \(30\;{\rm{km/h}}\) (xem hình vẽ).
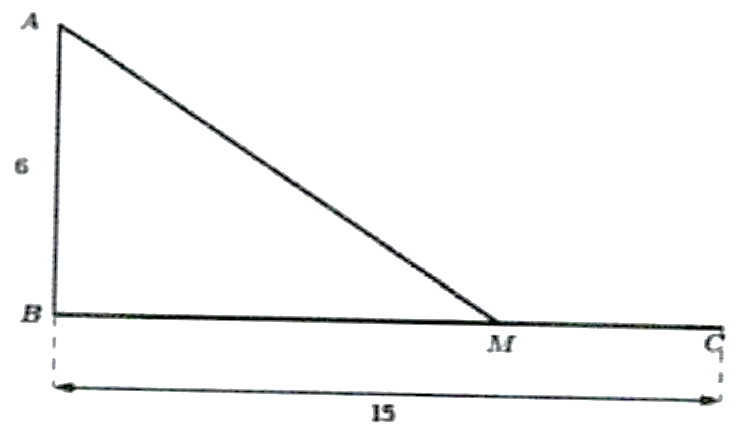
Tính tổng quãng đường người đó phải đi (đơn vị: km) biết rằng thời gian đi từ \(A\) đến \(C\) là 1 giờ 14 phút.
Một đường dây điện được nối từ nhà máy điện trên đất liền ở vị trí \(A\) đến một hòn đảo ở vị trí \(D\). Khoảng cách ngắn nhất từ \(D\) vào đất liền là \(DC = 2\,{\rm{km}}\). Khoảng cách từ \(A\) đến \(C\) là \(5\,{\rm{km}}\). Người ta chọn một vị trí (điểm\(B\)) nằm giữa \(A\) và \(C\) để mắc đường dây điện từ \(A\) đến \(B\), rồi từ \(B\) đến \(D\). Chi phí mắc mỗi kilômét dây điện trên đất liền là \(3000\,{\rm{USD}}\), chi phí mắc mỗi kilômét dây điện ngầm dưới biển là \(5000\,{\rm{USD}}\). Hỏi điểm \(B\) phải cách điểm \(A\) bao nhiêu kilômét, biết tổng chi phí mắc dây điện nối từ vị trí \(A\) đến vị trí \(D\) theo cách trên là \(23000\,{\rm{USD}}\).




