20 câu Trắc nghiệm Toán 10 Cánh diều Bài 3. Dấu của tam thức bậc hai (Đúng-sai, trả lời ngắn) có đáp án
20 câu hỏi
Tìm khẳng định đúng trong các khẳng định sau?
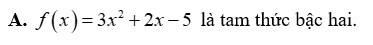
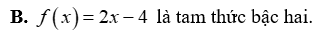
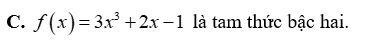
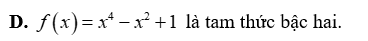
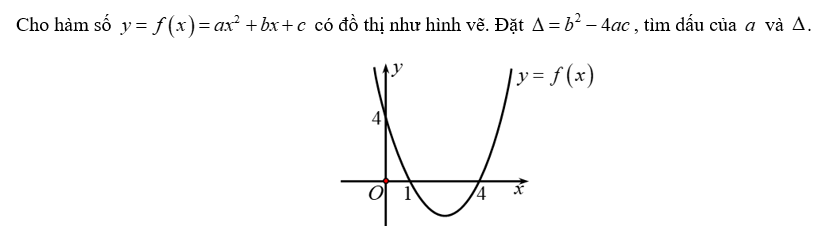
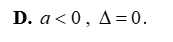
Tam thức nào sau đây luôn dương với mọi giá trị của x?
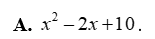
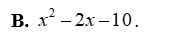
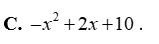
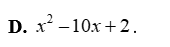
Tam thức bậc hai nào sau đây có hệ số \(a = 3;b = - 2;c = - 7\)?
\(3{x^2} - 2x - 7\).
\( - 3{x^2} + 2x + 7\).
\(3{x^2} - 2x + 7\).
\(3{x^2} + 2x - 7 = 0\).
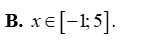
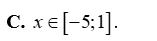
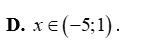
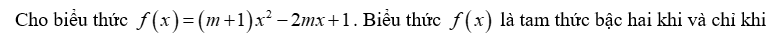
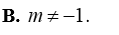
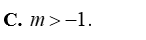
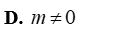
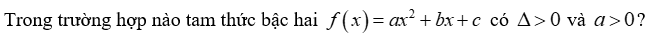
Hình 3.
Hình 4.
Hình 1.
Hình 2.
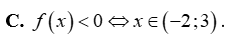
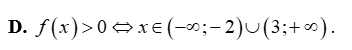
Tam thức bậc hai \(f\left( x \right) = {x^2} - 12x - 13\) nhận giá trị không âm khi và chỉ khi
\(x \in \left( { - 1;13} \right)\).
\(x \in \mathbb{R}\backslash \left[ { - 1;13} \right]\).
\(x \in \left[ { - 1;13} \right]\).
\(x \in \left( { - \infty ; - 1} \right] \cup \left[ {13; + \infty } \right)\).
D. \ (x \ in \ left ({ - \ infty; - 1} \ right] \ Cup \ left [{13; + \ infy} \ right) \).
Bảng xét dấu bên dưới là của tam thức bậc hai nào sau đây?
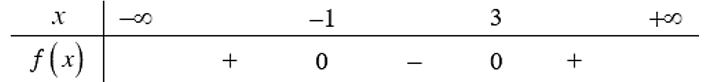
\(f\left( x \right) = {x^2} - 2x - 3\).
\(f\left( x \right) = - {x^2} + 2x + 3\).
\(f\left( x \right) = - {x^2} - 2x + 3\).
\(f\left( x \right) = {x^2} + 2x - 3\).
Cho hàm số \[f\left( x \right) = \left( {m - 1} \right){x^2} + x + 3\].
a) \(f\left( 0 \right) > 0\).
b) \(f\left( x \right)\) là tam thức bậc hai khi và chỉ khi \(m \ne 1\).
c) \(f\left( 1 \right) \ge 0\) khi và chỉ khi \(m \ge 3\).
d) Hàm số luôn nhận giá trị dương khi \(m > \frac{{13}}{{12}}\).
Tam thức bậc hai \(f\left( x \right) = {x^2} - ax + b\) có bảng xét dấu như hình vẽ:
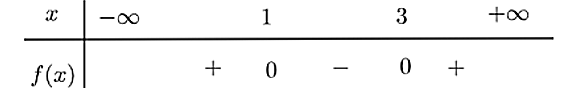
a) \(f\left( x \right) < 0 \Leftrightarrow 1 < x < 3\).
b) \(a + b = 7\).
c) \(f\left( 4 \right) = 3\).
d) Bảng xét dấu của đa thức \(g\left( x \right) = \left( {{x^2} - 3x + 2} \right)f\left( x \right)\) như sau:
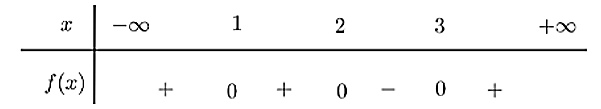
Cho tam thức \(f\left( x \right) = {x^2} - mx + m + 3\), với m là tham số thực.
a) Khi m = 2 thì tam thức có hai nghiệm phân biệt.
b) Khi m = 2 thì tam thức luôn âm với mọi \(x \in \mathbb{R}\).
c) Khi m = \( - 2\) thì tam thức luôn không âm với mọi \(x \in \mathbb{R}\).
d) Có 7 giá trị nguyên dương của tham số m để hàm số \(y = \frac{1}{{\sqrt {f\left( x \right)} }}\) luôn xác định với mọi \(x \in \mathbb{R}\).
Cho \(f\left( x \right) = {x^2} - 2\left( {m - 1} \right)x + {m^2} - 4\).
a) Nếu \(m = 1\) thì \(f\left( x \right)\) không phải là tam thức bậc hai.
b) Khi \(m = 3\) thì bất phương trình \(f\left( x \right) \le 0\) có tập nghiệm chứa hữu hạn giá trị nguyên.
c) Phương trình \(f\left( x \right) = 0\) có hai nghiệm trái dấu với \(\forall m \in \left( {a;b} \right)\). Khi đó \(a + b = 0\).
d) \(f\left( x \right)\) nhận giá trị không dương trên khoảng \(\left[ {a;\,b} \right]\) có \(b - a = 5\) khi m > 1.
Một công ty Du lịch sinh thái thông báo giá tiền khi tham gia chuyến tham quan của một nhóm khách du lịch được cho như sau:
Số khách | 20 khách đầu tiên | từ khách thứ 21 trở đi |
Giá tiền | 30 USD/người | Giảm 1 USD/người cho toàn bộ khách trong nhóm |
Gọi x là số lượng khách từ người thứ 21 trở đi của nhóm.
a) Số khách tham quan chuyến du lịch trên là \(20 - x\).
b) Giá vé của mỗi người là \(30 - x\).
c) Doanh thu của công ty được tính bởi công thức \( - {x^2} + 10x + 600\).
d) Biết chi phí của chuyến tham quan mà công ty phải chịu là 400 USD. Khi đó, nếu số khách từ người thứ 21 trở lên của nhóm nhiều hơn 20 người thì công ty có lãi.
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{1}{{\sqrt {2{x^2} - \left( {2m - 1} \right)x + 1} }}\) có tập xác định là \(\mathbb{R}\).
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để \(f\left( x \right) = \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x + m - 3\) không dương với mọi \(x \in \mathbb{R}\).
Một khung dây thép hình chữ nhật với chiều dài \(30\;{\rm{cm}}\) và chiều rộng \(20\;{\rm{cm}}\) được uốn lại thành hình chữ nhật mới với kích thước \(\left( {30 - x} \right)\)\({\rm{cm}}\) và \(\left( {20 + x} \right)\,\,{\rm{cm}}\), khi đó với \(x\) nằm trong khoảng \(\left( {a;\,b} \right)\) thì diện tích của khung sau khi uốn tăng lên. Tính giá trị biểu thức \(a + b\).
Một quả bóng được đá lên từ mặt đất, biết rằng chiều cao \(y\) (mét) của quả bóng so với mặt đất được biểu diễn bởi một hàm số bậc hai theo thời gian \(t\) (giây). Sau 3 giây kể từ lúc được đá lên, quả bóng đạt chiều cao tối đa là \(21\;\,{\rm{m}}\) và bắt đầu rơi xuống. Hỏi thời điểm \(t\) lớn nhất là bao nhiêu (\(t\) nguyên) để quả bóng vẫn đang ở độ cao trên \(10\;{\rm{m}}\) so với mặt đất?
Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của một nhóm khách như sau: 50 khách đầu tiên có giá 300 000 đồng/người.
Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm một người, giá vé sẽ giảm 5 000 đồng/người cho toàn bộ hành khách.
Biết chi phí thực sự của chuyến đi là 15 080 000 đồng. Số người của nhóm khách du lịch nhiều nhất là bao nhiêu để công ty không bị lỗ?




