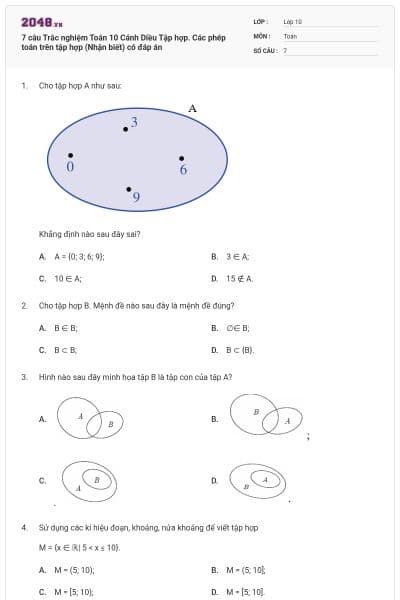
20 câu trắc nghiệm Toán 10 Cánh diều Bài 2. Tập hợp. Các phép toán trên tập hợp (Đúng sai - Trả lời ngắn) có đáp án
21 câu hỏi
Cho tập hợp \(A = \left\{ {x \in {\mathbb{N}^*},x < 10,\,\,x \vdots 3} \right\}\). Chọn khẳng định đúng.
\(A\) có \[4\] phần tử.
\(A\) có \[3\] phần tử.
\(A\) có \[5\] phần tử.
\(A\) có \[2\] phần tử.
Số tập con của tập hợp \(A = \left\{ {x \in \mathbb{R}|3{{\left( {{x^2} + x} \right)}^2} - 2{x^2} - 2x = 0} \right\}\) là:
16.
8.
12.
10.
Trong các tập hợp sau, tập hợp nào khác rỗng?
\[A = \left\{ {x \in \mathbb{R}\left| {{x^2} + x + 1 = 0} \right.} \right\}\].
\[B = \left\{ {x \in \mathbb{N}\left| {{x^2} - 2 = 0} \right.} \right\}\].
\[C = \left\{ {x \in \mathbb{Z}\left| {\left( {{x^3}--3} \right)\left( {{x^2} + 1} \right) = 0} \right.} \right\}\].
\[D = \left\{ {x \in \mathbb{Q}\left| {x\left( {{x^2} + 3} \right) = 0} \right.} \right\}\].
Cho ba tập hợp E, F, G thỏa mãn: \(E \subset F,F \subset G\) và \(G \subset K\). Khẳng định nào sau đây đúng?
\(G \subset F\).
\(K \subset G\).
\(E = F = G\).
\(E \subset K\).
Cho hai tập hợp: \(X = {\rm{ }}\left\{ {n \in \mathbb{N}|n} \right.\)là bội số của 4 và 6} và \(Y = {\rm{ }}\left\{ {n \in \mathbb{N}|n} \right.\)là bội số của 12}. Trong các mệnh đề sau, tìm mệnh đề sai?
\(X \subset Y\).
\(Y \subset X\).
\(X = Y\).
\(\exists n:\,n \in X\)và \(n \notin Y\).
Cho tập hợp \[A = \left\{ {1\,;\,2\,;\,3\,;\,4\,;\,x\,;\,y} \right\}\]. Xét các mệnh đề sau đây:
\[\left( I \right)\]: “\[3 \in A\]”.
\[\left( {II} \right)\]: “\[\left\{ {3\,;\,4} \right\} \in A\]”.
\[\left( {III} \right)\]: “\[\left\{ {x\,;\,3\,;\,y} \right\} \in A\]”.
Trong các mệnh đề sau, mệnh đề nào đúng?
\[I\] đúng.
\[I,II\] đúng.
\[II,III\] đúng.
\[I,III\] đúng.
Cho hai tập hợp \(X = \left\{ {1;2;3;4} \right\},Y = \left\{ {1;2} \right\}\). \({C_X}Y\) là tập hợp nào sau đây?
\(\left\{ {1;2} \right\}\).
\(\left\{ {1;2;3;4} \right\}\).
\(\left\{ {3;4} \right\}\).
\(\emptyset \).
Cho hai tập hợp \(A = \left\{ {0;2} \right\}\) và \(B = \left\{ {0;1;2;3;4} \right\}\). Số tập hợp X thỏa mãn \(A \cup X = B\) là:
2.
3.
4.
5.
Cho tập hợp \(A = \left\{ {1;2;3;4} \right\},B = \left\{ {0;2;4;6} \right\}\). Mệnh đề nào sau đây là đúng?
\(A \cap B = \left\{ {2;4} \right\}\).
\(A \cup B = \left\{ {0;1;2;3;4;5;6} \right\}\).
\(A \subset B\).
\(A\backslash B = \left\{ {0;6} \right\}\).
Cho hai tập \(A = \left[ {0;5} \right]\); \(B = \left( {2a;3a + 1} \right]\), \(a > - 1\). Với giá trị nào của \(a\) thì \(A \cap B \ne \emptyset \)?
\( - \frac{1}{3} \le a \le \frac{5}{2}\).
\(\left[ \begin{array}{l}a \ge \frac{5}{2}\\a < - \frac{1}{3}\end{array} \right.\).
\(\left[ \begin{array}{l}a < \frac{5}{2}\\a \ge - \frac{1}{3}\end{array} \right.\).
\( - \frac{1}{3} \le a < \frac{5}{2}\).
Cho hai tập hợp \(A = \left( {\sqrt 2 ; + \infty } \right)\) và \(B = \left( { - \infty ;\frac{{\sqrt 5 }}{2}} \right]\). Khi đó \(\left( {A \cap B} \right) \cup \left( {B\backslash A} \right)\) là
\(\left[ {\frac{{\sqrt 5 }}{2};\sqrt 2 } \right]\).
\(\left( {\sqrt 2 ; + \infty } \right)\).
\(\left( { - \infty ;\frac{{\sqrt 5 }}{2}} \right]\).
\(\left( { - \infty ;\frac{{\sqrt 5 }}{2}} \right)\).
Cho tập hợp \(X = \left\{ { - 3; - 1;0;1;3} \right\}\).
a) \( - 1\) là một phần tử của tập hợp \(X\).
b) Số tập hợp con của \(X\) có \(2\) phần tử là \(10\).
c) Tính chất đặc trưng của tập hợp \(X\) là \(X = \left\{ {x \in \mathbb{N}|2x + 1 \le 5} \right\}\).
d) Số tập con của tập hợp \(X\) là \(32\) tập hợp.
Cho các tập hợp sau:
\(A = \left\{ {\left. {x \in \mathbb{R}} \right|\left( {{x^2} + 7x + 6} \right)\left( {{x^2} - 4} \right) = 0} \right\};\,B = \left\{ {\left. {x \in \mathbb{N}} \right|2x \le 8} \right\};\,C = \left\{ {\left. {2x + 1} \right|x \in \mathbb{Z}, - 2 \le x \le 4} \right\}\).
a) Tập hợp \(A\) có 3 phần tử.
b) \(A \cup B = \left\{ { - 6; - 2; - 1;0;1;2;3;4} \right\}\).
c) \(A \cap B = \left\{ 2 \right\}\).
d) \(A \cup C = \left\{ { - 6; - 3; - 2;2;3;5;7;9} \right\}\).
Cho hai tập hợp \(A = \left[ { - 5;1} \right]\) và \(B = \left( { - 3;2} \right)\).
a) \(A \cup B = \left[ { - 3;2} \right)\).
b) \(A \cap B = \left( { - 3;2} \right]\).
c) \(A\backslash B = \left[ { - 5; - 3} \right]\).
d) \({C_\mathbb{R}}\left( {A \cup B} \right) = \left( { - \infty ; - 5} \right) \cup \left[ {1; + \infty } \right).\)
Một lớp có \[40\] học sinh, biết rằng ai cũng đăng kí thi ít nhất một trong hai môn là cờ vua và cờ tướng. Có \[17\] em đăng kí môn cờ vua, \[28\] em đăng kí môn cờ tướng.
a) Có \(28\) học sinh chỉ đăng kí môn cờ tướng.
b) Số học sinh chỉ đăng kí môn cờ vua là \[17\] học sinh.
c) Số học sinh đăng kí môn cờ tướng là \[28\]học sinh.
d) Có tất cả \(5\) học sinh đăng kí cả hai môn cờ.
Cho hai tập \(A = \left\{ {x \in \mathbb{R}|x + 2 \ge 0} \right\}\) và \(B = \left\{ {x \in \mathbb{R}|2x - 1 < 0} \right\}\).
a) \(A = \left[ { - 2; + \infty } \right)\), \(B = \left( { - \infty ;\frac{1}{2}} \right)\).
b) Biểu diễn trên trục số tập hợp \(A\) là
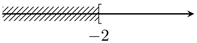c) \(A \cap B = \left( { - \infty ; + \infty } \right)\)d) Số phần tử nguyên của tập hợp \(A \cap B\) là 5.
Xác định số phần tử của tập hợp \(X = \left\{ {n \in \mathbb{N}|n\, \vdots \,4\,,\,n < 2017} \right\}\).
Cho tập hợp \(A = \left( { - \infty ; - 2} \right]\) và \(B = \left( { - 5;3} \right]\). Tính tổng các giá trị nguyên của tập hợp \(A \cap B\).
Cho hai tập hợp \(X,Y\) thỏa mãn \(X\backslash Y = \left\{ {7;15} \right\}\) và \(X \cap Y = \left( { - 1;2} \right)\). Xác định số phần tử là số nguyên của \(X\).
Bạn A.Súa thống kê số ngày có mưa, có sương mù ở bản mình trong tháng 3 vào một thời điểm nhất định và được kết quả như sau: 14 ngày
có mưa, 15 ngày có sương mù, trong đó 10 ngày có cả mưa và sương mù. Hỏi trong tháng 3 đó có bao nhiêu ngày không có mưa và không
có sương mù?
Trong lớp học có \(45\) học sinh trong đó có \(25\) học sinh thích môn Toán, \(20\) học sinh thích môn Anh, \(18\) học sinh thích môn Văn,
\(6\) học sinh không thích môn nào, \(5\) học sinh thích cả ba môn. Tổng số học sinh thích chỉ một trong ba môn Toán, Anh, Văn là bao
nhiêu?
