30 câu hỏi
Cho số phức , số phức liên hợp của z là
= 3 - 4i
= -3 + 4i
= -3 - 4i
= 1 + 2i
Cho hai số phức . Giá trị của biểu thức bằng
10
-6
4
Biết phương trình có một nghiệm là z = -2 + i. Tính a + b
9.
1.
4
-1
Cho số phức z thỏa mãn phương trình 4|z+i| + 3|z-i| = 10. Tính giá trị nhỏ nhất của |z|
1
Điểm nào trong hình vẽ dưới đây là điểm biễu diễn của số phức z = (1+i)(2-i)?
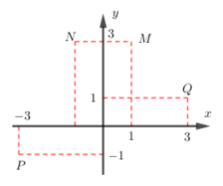
P
M
N
Q
Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn |+2-i| = 4 là đường tròn có tâm I và bán kính R lần lượt là
I(-2;-1), R = 4
I(-2;-1), R = 2
I(2;-1), R = 4
I(2;-1), R = 2
Cho số phức z = x + yi (a,b ) thỏa mãn . Tính P = x + y.
P = 7
P = -1
P = 1
P = 2
Điểm M trong hình vẽ là biểu diễn hình học của số phức nào dưới đây?
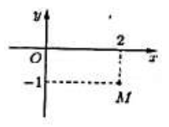
z = 2 - i
z = 2 + i
z = -1 + 2i
z = -1 - 2i
Tập hợp các điểm biểu diễn số phức z thỏa mãn |z-1+i| = 2 là đường tròn có tâm và bán kính lần lượt là
I(-1;1), R = 4
I(-1;1), R = 2
I(1;-1), R = 2
I(1;-1), R = 4
Gọi là hai nghiệm phức của phương trình + 2z + 10 = 0. Giá trị của bằng
20
2
10
Cho hai số thực x,y thỏa mãn x(3+2i) + y(1-4i) = 11+12i. Giá trị của x + y bằng
3.
-7.
–3.
7.
Tìm hai số thực x và y thỏa mãn (2x-3yi) + (1-3i) = x + 6i với i là đơn vị ảo.
x = -1; y = -3
x = -1; y = -1
x = 1; y = -1
x = 1; y = -3
Xét các số phức z thỏa mãn (+i)(z+2) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
1
Có bao nhiêu số phức z thỏa mãn |z|(z-4-i) + 2i = (5-i)z?
2
3
1
4
Số phức -3 + 7i có phần ảo bằng
3.
-7.
–3.
7.
Phần ảo của số phức z = 5 + 2i bằng:
5
5i
2
2i
Tập hợp các điểm biểu diễn số phức z thỏa mãn |z+2| = |z-i| là một đường thẳng có phương trình
4x + 2y + 3 = 0
2x + 4y + 13 = 0
2x - 4y + 13 = 0
Cho z là số phức thỏa mãn || = |z+2i|. Giá trị nhỏ nhất của |z-1+2i| + |z+1+3i| là
5
52
13
29
Cho số phức z = 6 + 7i. Số phức liên hợp của z là
= 6 + 7i
= -6 + 7i
= -6 - 7i
= 6 - 7i
Tính mô đun của số phức z, biết (1-2i)z + 2 - i = -12i
5
Cho số phức z thỏa mãn . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của |z-4+3i|. Giá trị M.m bằng
20
24
26
28
Tập hợp các điểm M biểu diễn số phức z sao cho là
Trục tung và trục hoành.
Trục tung.
Trục hoành.
Gốc tọa độ.
Gọi là hai nghiệm phức của phương trình . Khi đó phần thực của là
7.
5.
4.
6.
Cho hai số phức z, w thỏa mãn . Tìm gía trị nhỏ nhất của biểu thức P = |z-w|.
Pmin = 32-22
Pmin = 2 + 1
Pmin = 52-22
Pmin = 22+12
Cho các góc và có số phức z = cos + i.sin. Khi đó x = z.w thì:
x = cos(α-β) + i.sin(α+β)
x = cos(α+β) + i.sin(α+β)
x = cos(αβ) + i.sin(αβ)
x = sin(α-β) + i.cos(α+β)
Biết các số phức z,w khác 0 thỏa mãn: = zw Khi đó:
z6 = w6
z5 = w5
z4 = iw4
z3 + iw3 = 0
Biết số phức z thỏa mãn: là số thuần ảo. Khi đó ta phải có:
iz∉ℝ
|z| = 4
|z| = 1
z = 12 -i.32
Biết . Tìm a,b.
a = 0b = 1
a = 1b = 0
a = 1b = 1
a = -1b = -1
Tìm phần thực a của số phức
a = 1
a =
a =
a =
Biết z thỏa mãn |z - 2i + 1| thì |z + i| đạt giá trị nhỏ nhất là bao nhiêu? (z' = z + i)
|z|min = 3 - 5
|z|min = 13
|z|min =10 - 3
|z|min = 3 + 5

