15 CÂU HỎI
I. Nhân biết
Trong các hệ thức sau, hệ thức nào không phải là phương trình bậc nhất hai ẩn?
\[2x + 3y = - 5.\]
\[0x - 7y = 1.\]
\[0x + 0y = 2.\]
\[4x - 0y = 11.\]
Hệ số \[a,b\] và \[c\] tương ứng của phương trình bậc nhất hai ẩn \[ - 7x - 12 = 0\] là
\[a = - 7,b = 0,c = 12.\]
\[a = - 7,b = - 12,c = 0.\]
\[a = 0,b = - 7,c = 12.\]
\[a = 0,b = - 12,c = 0.\]
Cặp số nào sau đây là nghiệm của phương trình \[3x - 2y + 1 = 0?\]
\[\left( { - 1;1} \right).\]
\[\left( {5;3} \right).\]
\[\left( {0;1} \right).\]
\[\left( { - 1; - 1} \right).\]
Cho hệ phương trình \[\left\{ \begin{array}{l}2x + 9y = 10\\5y - 3x = - 6\end{array} \right.,\] hệ số \[a,b,c\] và \[a',b',c'\] của hệ phương trình theo dạng hệ hai phương trình bậc nhất một ẩn là
\[a = 9,b = 10,c = 2\] và \[a' = 5,b' = - 3,c' = - 6.\]
\[a = 2,b = 9,c = 10\] và \[a' = - 3,b' = 5,c' = - 6.\]
\[a = 9,b = 2,c = - 10\] và \[a' = 5,b' = 3,c' = - 6.\]
\[a = 2,b = 9,c = 10\] và \[a' = - 3,b' = - 5,c' = 6.\]
Cặp số \[\left( {1; - 5} \right)\] là nghiệm của hệ phương trình nào trong các hệ phương trình sau đây?
\[\left\{ \begin{array}{l}x - 5y = 13\\x - y = 3.\end{array} \right.\]
\[\left\{ \begin{array}{l}x - 5y = 13\\2x - 3y = - 1.\end{array} \right.\]
\[\left\{ \begin{array}{l}x - y = 6\\2x + y = - 3.\end{array} \right.\]
\[\left\{ \begin{array}{l}x + y = 8\\x - y = 3.\end{array} \right.\]
II. Thông hiểu
Mỗi nghiệm của phương trình \[7x + 0y = 4\] được biểu diễn bởi một điểm nằm trên đường thẳng có đồ thị là hình vẽ nào trong các hình vẽ sau?
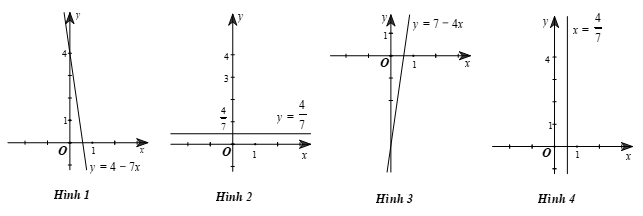
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Điểm \[M\left( {1;3} \right)\] không thuộc đường thẳng nào sau đây?
\[3x + y = - 4.\]
\[3x - y = - 1.\]
\[3x - y = 5.\]
\[3x + y = 6.\]
Với giá trị nào của \[{x_0}\] để cặp số \[\left( {{x_0}; - 2} \right)\] là nghiệm của phương trình \[x - 7y = 21?\]
\[{x_0} = 7.\]
\[{x_0} = - 1.\]
\[{x_0} = - 2.\]
\[{x_0} = 2.\]
Cho hệ phương trình \[\left\{ \begin{array}{l} - x - 3y = 2\\5x + 9y = - 11\end{array} \right..\] Khi giải hệ phương trình bằng phương pháp thế (biểu diễn \(x\) theo \(y)\), ta được phương trình ẩn \(y\) là
\[ - 6y = - 21.\]
\[y = - 3y - 2.\]
\[ - 6y = - 1.\]
\[6y = - 1.\]
Cho hệ phương trình \[\left\{ \begin{array}{l}x - 7y = m\\ - mx + 2y = 9\end{array} \right..\] Khi \[m = 1\] thì hệ phương trình đã cho có nghiệm là
\[\left( {13;2} \right).\]
\[\left( { - 13; - 2} \right)\].
\[\left( {13; - 2} \right)\].
\[\left( {2; - 13} \right).\]
Cho hệ phương trình \[\left\{ \begin{array}{l}\left( {x - 1} \right)\left( {y + 1} \right) = xy + 4\\\left( {x + 2} \right)\left( {y - 1} \right) = xy - 10\end{array} \right..\] Nghiệm của hệ phương trình trên là
\[\left( {x;y} \right) = \left( {2;3} \right).\]
\[\left( {x;y} \right) = \left( {2; - 3} \right).\]
\[\left( {x;y} \right) = \left( { - 2; - 3} \right).\]
\[\left( {x;y} \right) = \left( { - 2;3} \right).\]
Để giải hệ phương trình \[\left\{ \begin{array}{l}x - 7y = 9\\3x - 5y = 6\end{array} \right.\] bằng máy tính cầm tay, ta ấn liên tiếp các phím:
![Để giải hệ phương trình \[\left\{ \begin{array}{l}x - 7y = 9\\3x - 5y = 6\end{array} \right.\] bằng máy tính cầm tay, ta ấn liên tiếp các phím: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid1-1728619608.png)
![Để giải hệ phương trình \[\left\{ \begin{array}{l}x - 7y = 9\\3x - 5y = 6\end{array} \right.\] bằng máy tính cầm tay, ta ấn liên tiếp các phím: (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid2-1728619617.png){kind=small}
![Để giải hệ phương trình \[\left\{ \begin{array}{l}x - 7y = 9\\3x - 5y = 6\end{array} \right.\] bằng máy tính cầm tay, ta ấn liên tiếp các phím: (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid3-1728619640.png){kind=small}
![Để giải hệ phương trình \[\left\{ \begin{array}{l}x - 7y = 9\\3x - 5y = 6\end{array} \right.\] bằng máy tính cầm tay, ta ấn liên tiếp các phím: (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid4-1728619659.png){kind=small}
III. Vận dụng
Với giá trị dương nào của \[m\] thì phương trình \[2x - {\left( {m - 2} \right)^2}y = 5\] nhận cặp số \[\left( { - 10; - 1} \right)\] làm nghiệm?
\[m = 3.\]
\[m = - 3.\]
\[m = 7.\]
\[m = 7\] hoặc \[m = - 3.\]
Hai ngăn của một kệ sách có tổng cộng \[500\] cuốn sách. Nếu chuyển \[75\] cuốn sách từ ngăn thứ nhất sang ngăn thứ hai thì số sách ở ngăn thứ hai gấp \[3\] lần số sách ở ngăn thứ nhất. Khi đó số sách ở ngăn thứ nhất và ngăn thứ hai ban đầu lần lượt là
\[200\] và \[300.\]
\[250\] và \[250.\]
\[300\] và \[200.\]
\[400\] và \[100.\]
Cho hệ phương trình \(\left\{ \begin{array}{l}x - my = 1\\mx + y = 3\end{array} \right.\) với \(m\) là tham số và \(\left( {{x_0};\,\,{y_0}} \right)\) là nghiệm của hệ phương trình. Giá trị của biểu thức \(P = x_0^2 + y_0^2 - {x_0} - 3{y_0}\) là
\(P = - 1\).
\(P = 0\).
\(P = 1\).
\(P = 2\).