15 câu hỏi
I. Nhận biết
Đa giác đều trong các hình dưới đây là
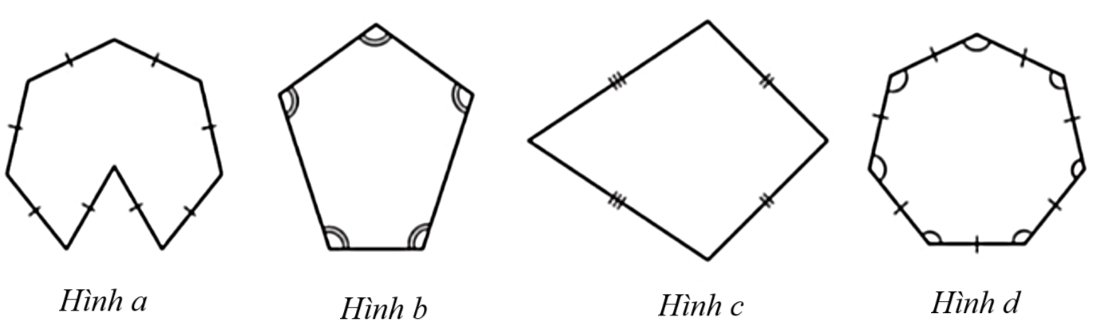
Hình a.
Hình b.
Hình c.
Hình d.
Khẳng định nào sau đây là sai?
Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Trong một đường tròn, số đo của góc nội tiếp bằng số đo của cung bị chắn.
Đường tròn ngoại tiếp đa giác là đường tròn
Tiếp xúc tất cả các cạnh của đa giác đó.
Đi qua tất cả các đỉnh của đa giác đó.
Cắt tất cả các cạnh của đa giác đó.
Đi qua tâm của đa giác đó.
Trong các hình sau, hình nội tiếp được trong đường tròn là:
Hình thang, hình chữ nhật.
Hình thang cân, hình bình hành.
Hình thoi, hình vuông.
Hình thang, hình chữ nhật, hình vuông.
Trong các hình sau,hình đang nội tiếp đường tròn là
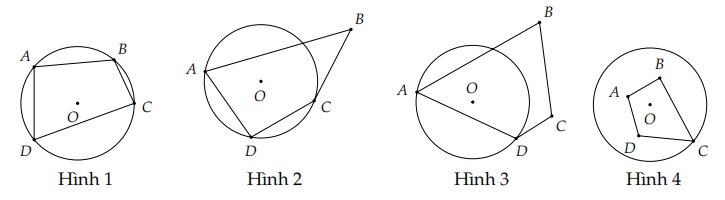
Hình 1.
Hình 2.
Hình 3.
Hình 4.
II. Thông hiểu
Phép quay với \[O\] là tâm biến tam giác đều thành chính nó là phép quay thuận chiều một góc:
\(90^\circ \).
\(100^\circ \).
\(110^\circ \).
\(120^\circ \).
Khi tứ giác \[MNPQ\] nội tiếp đường tròn, và có \(\widehat M = 90^\circ \). Khi đó, góc \[P\] bằng
\(90^\circ \).
\(180^\circ \).
\(110^\circ \).
\(120^\circ \).
Tam giác đều \[ABC\] nội tiếp đường tròn. Khi đó góc \[AOB\] bằng
\(120^\circ \).
\(60^\circ \).
\(140^\circ \).
\(80^\circ \).
Cho đường tròn \[\left( O \right)\]. Trên \[\left( O \right)\] lấy ba điểm \[A,{\rm{ }}B,{\rm{ }}D\] sao cho \(\widehat {AOB} = 120^\circ \), \[AD = BD\]. Khi đó tam giác \[ABD\] là
tam giác đều.
tam giác vuông tại \[D\].
tam giác vuông cân tại \[D\].
tam giác vuông tại \[A\].
Cho tứ giác \[ABCD\] nội tiếp một đường tròn \[\left( O \right)\]. Biết \(\widehat {BOD} = 140^\circ \). Số đo góc \(\widehat {BCD}\) là
\(110^\circ \).
\(70^\circ \).
\(140^\circ \).
\(290^\circ \).
Cho tam giác \[ABC\] có ba góc nhọn, đường cao \[AH\] và nội tiếp đường tròn tâm \[\left( O \right)\], đường kính \[AM\]. Gọi \[N\] là giao điểm của \[AH\] với đường tròn \[\left( O \right)\]. Tứ giác \[BCMN\] là
Hình thang.
Hình thang vuông.
Hình thang cân.
Hình bình hành.
Cho tam giác \[ABC\] nhọn nội tiếp \[\left( O \right)\]. Hai đường cao \[BD\] và \[CE\] cắt nhau tại \[H\]. Vẽ đường kính \[AF\]. Khẳng định nào sau đây là đúng?
\[BH = BE\].
\[BH = CF\].
Cả A và B đều đúng.
Cả A và B đều sai.
III. Vận dụng
Tứ giác \[ABCD\] nội tiếp đường tròn có hai cạnh đối \[AB\] và \[CD\] cắt nhau tại \[M\] và \(\widehat {BAD} = 70^\circ \). Số đo \(\widehat {BCM}\) là
\(60^\circ \).
\(70^\circ \).
\(80^\circ \).
\(90^\circ \).
Cho lục giác đều \[ABCDEF\] tâm \(O\) biết \[OA = 4{\rm{ cm}}.\] Độ dài mỗi cạnh của lục giác đều \[ABCDEF\] là bao nhiêu?
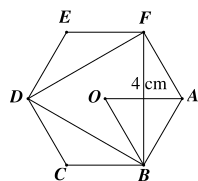
\[8{\rm{ cm}}.\]
\[5{\rm{ cm}}.\]
\[4{\rm{ cm}}.\]
\[2{\rm{ cm}}.\]
Cho ngũ giác đều \[MNPQR\] có tâm \[O.\] Phép quay nào với tâm \[O\] biến ngũ giác đều \[MNPQR\] thành chính nó?
\[60^\circ .\]
\[72^\circ .\]
\[90^\circ .\]
\[120^\circ .\]
