15 câu hỏi
I. Nhận biết
Hình chữ nhật có chiều dài \[8{\rm{\;cm}},\] chiều rộng \[6{\rm{\;cm}}.\] Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có chiều cao \[h\] và bán kính đáy \[r.\]
Kết luận nào sau đây là đúng?
\[r = 8{\rm{\;cm}};\,\,h = 6{\rm{\;cm}}.\]
\[r = 4{\rm{\;cm}};\,\,h = 3{\rm{\;cm}}.\]
\[r = 3{\rm{\;cm}};\,\,h = 4{\rm{\;cm}}.\]
\[r = 6{\rm{\;cm}};\,\,h = 8{\rm{\;cm}}.\]
Một ống nước có dạng hình trụ (như hình vẽ).
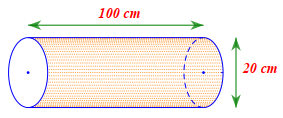
Kết luận nào sau đây là đúng?
Chiều cao của hình trụ là \[20{\rm{\;cm}}\] và bán kính đáy là \[10{\rm{\;cm}}.\]
Chiều cao của hình trụ là \[50{\rm{\;cm}}\] và bán kính đáy là \[20{\rm{\;cm}}.\]
Chiều cao của hình trụ là \[100{\rm{\;cm}}\] và bán kính đáy là \[10{\rm{\;cm}}.\]
Chiều cao của hình trụ là \[100{\rm{\;cm}}\] và bán kính đáy là \[20{\rm{\;cm}}.\]
Gọi \[h,\,\,r\] lần lượt là chiều cao và bán kính đáy của hình trụ \[\left( T \right).\] Thể tích \[V\] của hình trụ \[\left( T \right)\] có công thức là
\[V = \frac{4}{3}\pi {r^2}h.\]
\[V = \frac{2}{3}\pi {r^2}h.\]
\[V = \pi {r^2}h.\]
\[V = \frac{1}{3}\pi {r^2}h.\]
Gọi \[l,h,r\] lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ \[\left( T \right).\] Diện tích xung quanh \[{S_{xq}}\] của hình trụ \[\left( T \right)\] có công thức là
\[{S_{xq}} = 2\pi rl.\]
\[{S_{xq}} = \pi rl.\]
\[{S_{xq}} = \pi {r^2}h.\]
\[{S_{xq}} = \pi rh.\]
Gọi \[l,h,r\] lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ \[\left( T \right).\] Diện tích toàn phần \[{S_{tp}}\] của hình trụ \[\left( T \right)\] có công thức là
\[{S_{tp}} = \pi rl + \pi {r^2}.\]
\[{S_{tp}} = 2\pi rh + 2\pi {r^2}.\]
\[{S_{tp}} = \pi rh + \pi {r^2}.\]
\[{S_{tp}} = \pi rl + 2\pi {r^2}.\]
II. Thông hiểu
Một hình trụ có đường kính đáy \[2{\rm{\;dm}},\] đường sinh \[14{\rm{\;dm}}.\] Thể tích của hình trụ đó bằng
\[14\pi {\rm{\;d}}{{\rm{m}}^3}.\]
\[56\pi {\rm{\;d}}{{\rm{m}}^3}.\]
\[28\pi {\rm{\;d}}{{\rm{m}}^3}.\]
\[7\pi {\rm{\;d}}{{\rm{m}}^3}.\]
Cho hình chữ nhật có chiều dài \[3{\rm{\;cm}},\] chiều rộng \[2{\rm{\;cm}}.\] Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có diện tích xung quanh bằng
\[6\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[12{\rm{\;c}}{{\rm{m}}^2}.\]
\[12\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[18\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Cho hình chữ nhật \[MNPQ\] có \[MN = 16{\rm{\;cm}},NP = 12{\rm{\;cm}}.\] Khi quay hình chữ nhật đã cho một vòng quanh cạnh \[MN\] ta được một hình trụ có diện tích toàn phần (lấy \[\pi \approx 3,14)\] khoảng
\[2\,\,813,44{\rm{\;c}}{{\rm{m}}^2}.\]
\[1\,\,055,04{\rm{\;c}}{{\rm{m}}^2}.\]
\[2\,\,110,08{\rm{\;c}}{{\rm{m}}^2}.\]
\[1\,\,205,76{\rm{\;c}}{{\rm{m}}^2}.\]
Cho hình chữ nhật có chiều dài \[10{\rm{\;cm}},\] chiều rộng \[7{\rm{\;cm}}.\] Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có thể tích bằng
\[700\pi {\rm{\;c}}{{\rm{m}}^3}.\]
\[490\pi {\rm{\;c}}{{\rm{m}}^3}.\]
\[980\pi {\rm{\;c}}{{\rm{m}}^3}.\]
\[\frac{{490\pi }}{3}{\rm{\;c}}{{\rm{m}}^3}.\]
Cho hình trụ có bán kính đáy \[r = 8{\rm{\;cm}}\] và diện tích toàn phần \[564\pi {\rm{\;c}}{{\rm{m}}^2}.\] Chiều cao của hình trụ bằng
\[27,25{\rm{\;cm}}.\]
\[32,25{\rm{\;cm}}.\]
\[70,5{\rm{\;cm}}.\]
\[{\rm{54,5\;cm}}.\]
Cho hình trụ có chiều cao \[h = 12{\rm{\;cm}}\] và diện tích xung quanh \[{S_{xq}} = 64\pi {\rm{\;c}}{{\rm{m}}^2}.\] Bán kính đáy của hình trụ là
\[\frac{8}{3}{\rm{\;cm}}.\]
\[\frac{{4\sqrt 3 \pi }}{3}{\rm{\;cm}}.\]
\[\frac{{4\pi }}{3}{\rm{\;cm}}.\]
\[\frac{{8\pi }}{3}{\rm{\;cm}}.\]
Nếu tăng bán kính đáy của hình trụ lên 4 lần và giữ nguyên chiều cao thì thể tích mới của hình trụ
gấp 4 lần thể tích cũ.
gấp 8 lần thể tích cũ.
gấp 12 lần thể tích cũ.
gấp 16 lần thể tích cũ.
III. Vận dụng
Một hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \[h = 12{\rm{\;cm}}\] và đường kính đáy \[d = 8{\rm{\;cm}}.\] Diện tích toàn phần của hộp sữa là
\[96\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
\[110\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
\[112\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
\[128\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Cho hình trụ nằm bên trong hình lập phương có cạnh bằng \[x\] (hình vẽ).
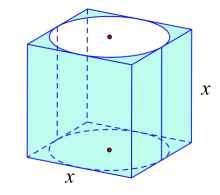
Tỉ số thể tích của hình trụ và hình lập phương đã cho là
\[\frac{\pi }{2}.\]
\[\frac{\pi }{4}.\]
\[\frac{\pi }{{12}}.\]
\[\frac{{2\pi }}{3}.\]
Một hình trụ \[\left( T \right)\] được tạo ra khi quay hình chữ nhật \[ABCD\] một vòng quanh cạnh \[AB.\] Biết \[AC = 2a\sqrt 2 \] và \[\widehat {ACB} = 45^\circ .\] Thể tích \[V\] của hình trụ \[\left( T \right)\] là
\[V = 16\pi {a^3}.\]
\[V = 8\pi {a^3}.\]
\[V = 4\pi {a^3}.\]
\[V = 12\pi {a^3}.\]
