15 câu hỏi
Chọn đáp án sai. Hai góc kề nhau là:
hai góc có đỉnh chung;
có một cạnh chung;
hai góc không chung đỉnh;
có hai cạnh nằm về hai phía của đường thẳng chứa cạnh chung.
Hai góc bù nhau là hai góc có tổng số đo bằng:
120°;
90°;
60°;
120°.
Trong các hình dưới đây hình nào là 2 góc kề bù.
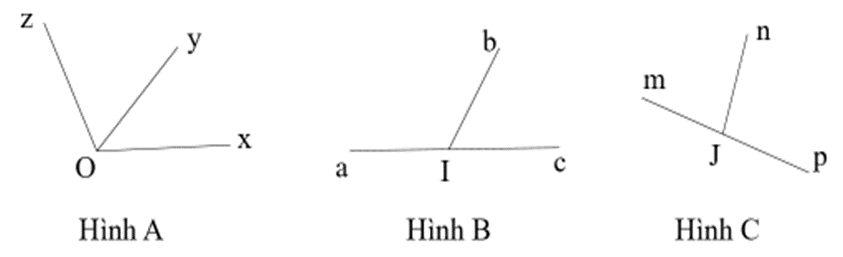
Hình A, B;
Hình B, C;
Hình A, C;
Không có hình nào.
Tìm số đo x:
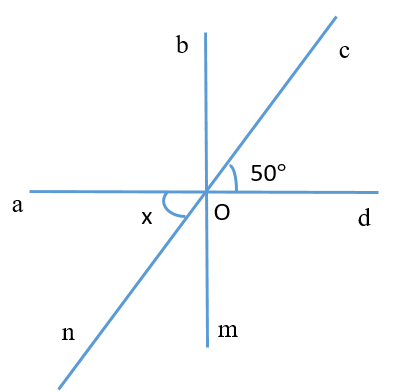
40°;
120°;
30°;
50°.
Hai góc đối đỉnh thì:
bằng nhau;
có tổng bằng 180°;
kề nhau;
có hiệu bằng 180°.
Quan sát hình bên và chỉ ra hai góc kề nhau.
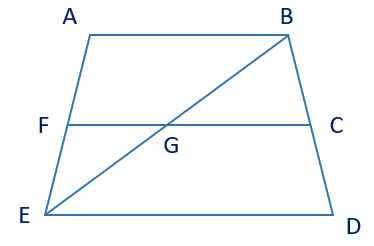
góc FGB và góc BGC;
góc FGB và góc EGC;
góc FAB và góc GBC;
góc BGC và góc FGE.
Tìm số đo x và y trong hình vẽ dưới đây:
x = 38° và y = 52°;
x = 38° và y = 142°;
x = 142° và y = 38°;
x = 52° và y = 38°.
Chọn đáp án đúng.

\[\widehat {ABC}\]và \[\widehat {CDE}\] là hai góc kề nhau;
\[\widehat {BGC}\] và \[\widehat {FGE}\] là hai góc kề nhau;
\[\widehat {CGE}\]và \[\widehat {FGB}\] là hai góc kề nhau;
\[\widehat {CGE}\] và \[\widehat {EGF}\] là hai góc kề nhau.
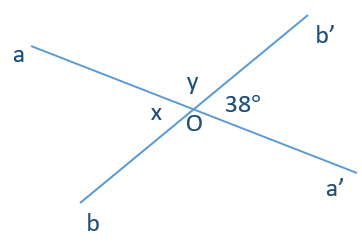
Góc aOb và góc b’Oa’ là:
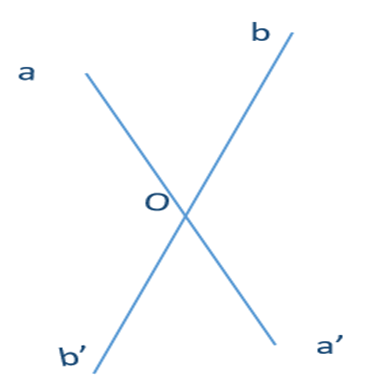
hai góc đối đỉnh;
hai góc kề nhau;
hai góc bù nhau;
hai góc kề bù.
Cho hình vẽ. Em hãy chỉ ra 2 góc đối đỉnh (khác góc bẹt).
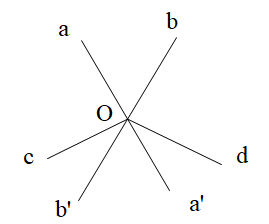
\(\widehat {aOb}\) và \(\widehat {aOb'}\);
\(\widehat {cOb'}\) và \(\widehat {bOd}\);
\(\widehat {aOb}\) và \(\widehat {a'Ob'}\);
\(\widehat {aOb'}\) và \(\widehat {aOd}.\)
Trong các hình dưới đây hình nào vẽ hai góc kề nhau là không đúng.
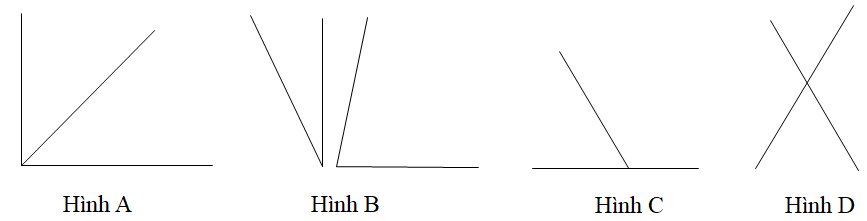
Hình A;
Hình B;
Hình C;
Hình D.
Tính góc xOz
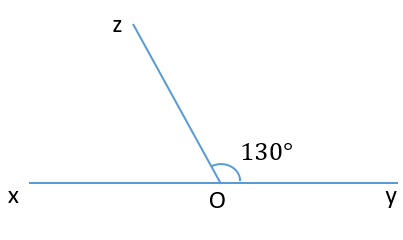
70°;
130°;
50°;
120°.
Trong các hình dưới đây hình nào vẽ hai góc kề bù
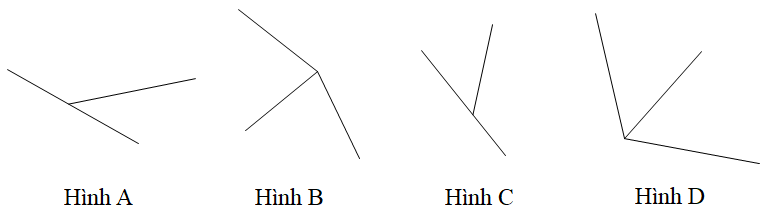
Hình A và Hình B;
Hình B và Hình C;
Hình C và Hình D;
Hình A và Hình C.
Chọn câu trả lời đúng.
Hai góc bù nhau là hai góc có tổng số đo bằng 180o;
Hai góc kề nhau là hai góc có tổng số đo bằng 180o;
Hai góc đối đỉnh là hai góc có tổng số đo bằng 180o;
Hai góc kề bù là hai góc có tổng số đo bằng 90o.
Cho cặp góc đối đỉnh \[\widehat {tOz}\] và \[\widehat {t'Oz'}\] (Oz và Oz’ là hai tai đối nhau). Biết \[3.\widehat {tOz'} = \widehat {tOz}\]. Tính các góc \[\widehat {tOz}\] và \[\widehat {t'Oz'}\].
\[\widehat {tOz} = \widehat {t'Oz'} = 45^\circ \];
\[\widehat {tOz} = \widehat {t'Oz'} = 105^\circ \];
\[\widehat {tOz} = \widehat {t'Oz'} = 135^\circ \];
\[\widehat {t'Oz'} = 135^\circ ,\;\widehat {tOz} = 45^\circ \].
