12 bài tập Tính bán kính đường tròn có lời giải
12 câu hỏi
Tính bán kính R của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh 3 cm.
R = \(3\sqrt 2 \) cm.
R = \(\frac{{3\sqrt 2 }}{2}\) cm.
R = 3 cm.
R = \(\frac{{3\sqrt 3 }}{2}\) cm.
Cho tam giác ABC vuông tại A, có AB = 15 cm, AC = 20 cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
R = 25.
R = \(\frac{{25}}{2}\).
R = 15.
R = 20.
Cho tam giác ABC vuông tại A có AB = 5 cm; AC = 12 cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
R = 26.
R = 13.
R = \(\frac{{13}}{2}\).
R = 6.
Cho hình chữ nhật ABCD có AB = 12 cm, BC = 5 cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D.
R = 7,5 cm.
R = 13 cm.
R = 6 cm.
R = 6,5 cm.
Cho hình chữ nhật ABCD có AB = 8 cm, BC = 6 cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D.
R = 5 cm.
R = 10 cm.
R = 6 cm.
R = 2,5 cm.
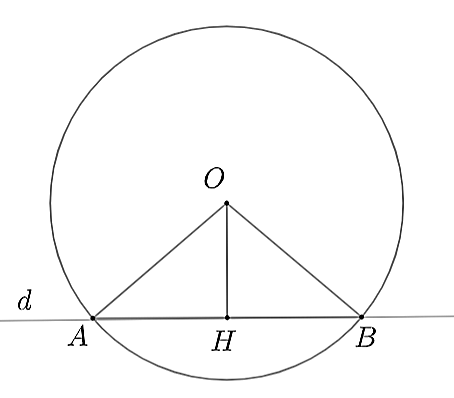
Cho đường tròn tâm O và đường thẳng d cắt đường tròn (O) tại hai điểm A và B sao cho AB = 4 cm và khoảng cách từ tâm O đến đường thẳng d là 1 cm. Tính bán kính đường tròn (O).
\(\sqrt 3 \)cm.
\(\sqrt 5 \) cm.
\(\frac{{\sqrt 5 }}{2}\) cm.
\(\frac{{\sqrt 3 }}{2}\)
Cho tam giác ABC cạnh bằng 4 cm, các đường cao là BM và CN. Gọi D là trung điểm cạnh BC. Bán kính của đường tròn đi qua bốn điểm B, N, M, C là:
2 cm.
4 cm.
6 cm.
8 cm.
Cho hình cuông ABCD cạnh 4 cm. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là giao điểm của CM và DN. Bán kính của đường tròn đi qua bốn điểm A, D, E, M là
R = 5 cm.
R = 10 cm.
R = \(2\sqrt 5 \) cm.
R = \(\sqrt 5 \) cm.
Cho tam giác ABC cân ở A, đường cao AH = 2 cm, BC = 8 cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D. Tính đường kính của đường tròn đi qua các điểm A, B, C, D.
d = 8 cm.
d = 12 cm.
d = 10 cm..
d = 5 cm.
Cho tam giác đều ABC. Biết rằng đường tròn (O; 4cm) đi qua ba đỉnh của tam giác. Tính diện tích tam giác ABC.
24 cm2.
\(24\sqrt 3 \) cm2.
12 cm2.
\(12\sqrt 3 \) cm2.
Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Chứng minh rằng ba điểm A, B, C cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Cho hình vuông ABCD có E là giao điểm của hai đường chéo.
a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C, D. Xác định tâm đối xứng và hai trục đối xứng của đường tròn đó.
b) Tính bán kính của đường tròn đó nếu hình vuông có cạnh bằng 3 cm.


