10 câu hỏi
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \[y = \frac{{mx - 8}}{{x + 2}}\] có hai đường tiệm cận.
m ≠ 4;
m ≠ −4;
m = 4;
m = −4.
Cho hàm số \(y = \frac{{ax + 1}}{{bx - 2}}.\) Tìm a, b để đồ thị hàm số có x = 1 là tiệm cận đứng và \(y = \frac{1}{2}\) là tiệm cận ngang.
a = −1; b = 2;
a = 4; b = 4;
a = 1; b = 2;
a = −1; b = −2.
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số \(y = \frac{{{x^2} + m}}{{{x^2} - 3x + 2}}\) có đúng hai đường tiệm cận.
m = −1;
m ∈ {1; 4};
m = 4;
m ∈ {−1; −4}.
Tìm tất cả giá trị của tham số m để đường tiệm cận xiên của đồ thị hàm số \(y = 2mx + 3 - \frac{4}{{x + 1}}\) đi qua điểm M(1; 7).
m = 1;
m = 3;
m = 2;
m = −2.
Biết rằng đồ thị của hàm số \(y = \frac{{\left( {n - 3} \right)x + n - 2017}}{{x + m + 3}}\) (m, n là các số thực) nhận trục hoành làm tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng m + n.
0;
−3;
3;
6.
Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - 8x + m}}\] có 3 đường tiệm cận?
14;
8;
15;
16.
Cho đồ thị hàm số y = f(x) có bảng biến thiên xác định như hình. Biết rằng đồ thị hàm số có tiệm cận đứng x = x0, tiệm cận ngang là y = y0 và x0y0 = 16. Hỏi m bằng?
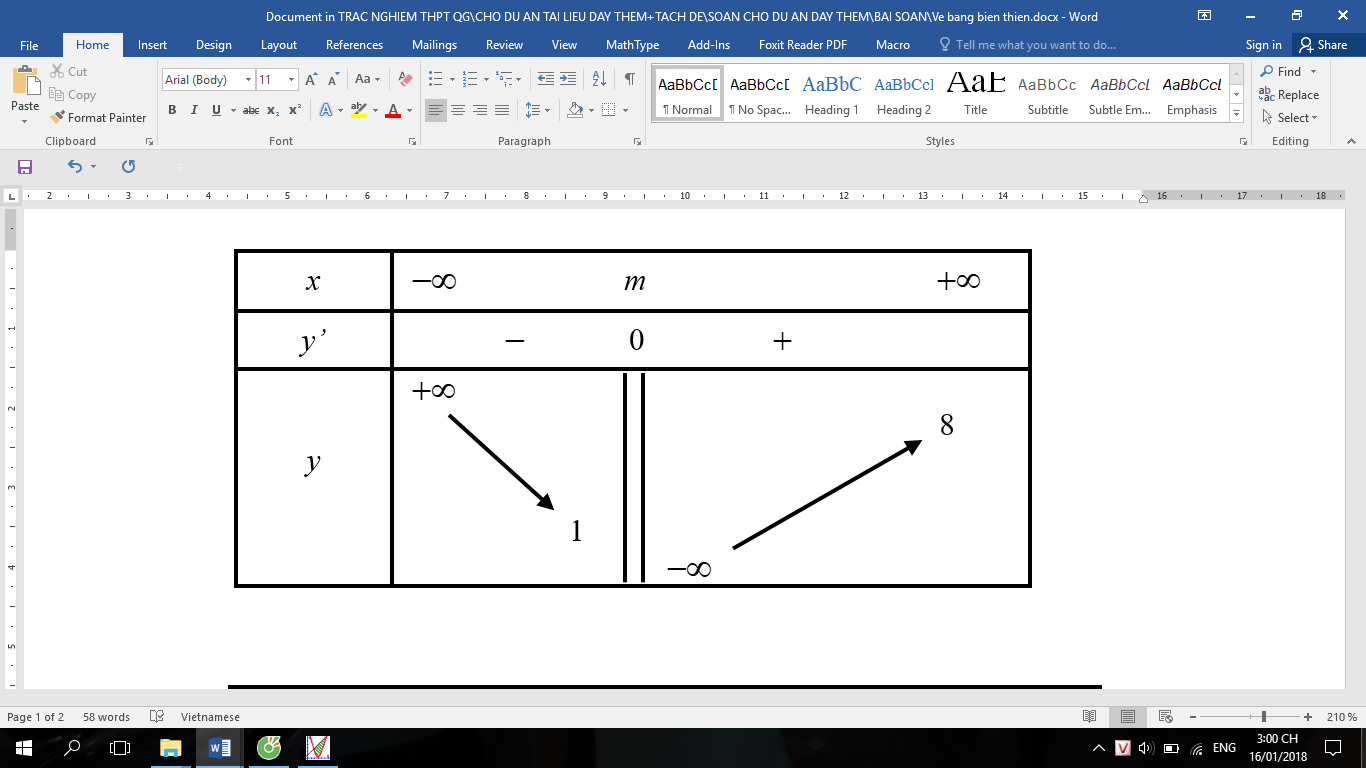
m = 8;
m = −16;
m = 1;
m = 2.
Cho hàm số y = f(x) có bảng biến thiên:
![Cho hàm số y = f(x) có bảng biến thiên: Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để hàm số có 4 tiệm cận? (ảnh 1)](https://video.vietjack.com/upload2/images/1742397066/1742397854-image3.png)
Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để hàm số có 4 tiệm cận?
5;
6;
7;
8.
Cho hàm số y = f(x) có bảng biến thiên sau:

Tìm tổng số các giá trị nguyên dương của tham số m ∈ (−10; 10) để đồ thị hàm số y = f(x) có tổng số đường tiệm cận đứng và đường tiệm cận ngang là 4.
42;
45;
−3;
0.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Định tham số m để giao điểm của đường tiệm cận đứng và tiệm cận ngang là điểm I(−1; 1).
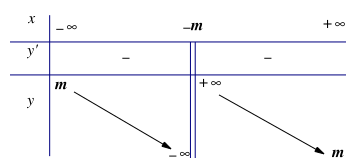
Không có m;
m = 0;
m = −1;
m = 1.
