118 câu Bài tập Hình học Khối đa diện cơ bản, nâng cao có lời giải chi tiết (P3)

Cho hình trụ thiết diện qua trục hoành là hình vuông ABCD cạnh $4\sqrt{3}$cm với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung AB sao cho $\widehat{ABM}= {60}^o$. Tính thể tích của khối tứ diện ACDM.

Cho hình lăng trụ đứng tam giác ABC.A'B'C' tam giác ABC có AB=a,AC = $a\sqrt{2}$, góc $\widehat{BAC}={60}^o$, A'C=$a\sqrt{3}$. Tính thể tích khối lăng trụ ABC.A'B'C' là

Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB = 4,AD = 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.

Cho khối đa diện đều n mặt có thể tích là V và diện tích mỗi mặt của nó là S. Khi đó tổng khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng

Cho hình chóp S.ABC có các cạnh SA=SB=SC=BA=BC=a. Tìm thể tích lớn nhất của hình chóp S.ABC.

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh S_xq của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ có đáy là hình tròn nội tiếp hình vuông ABCD là

Cho lăng trụ ABCA’B’C’, đáy là tam giác đều là cạnh bằng a, tứ giác ABB’A’ là hình thoi, $\widehat{A\text{'}AC}={60}^o$, $B\text{'}C=\frac{a\sqrt{3}}{2}$ Tính thể tích lăng trụ ABCA’B’C’.

Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là 

Cho hình lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng ${60}^o$, cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A'B'C' là

Hình hộp chữ nhật có độ dài ba cạnh xuất phát từ một đỉnh lần lượt là 3, 4, 5. Thể tích của hình hộp đó là

Cho hình lập phương ABCD.A'B'C'D' có các cạnh bằng 1. M là trung điểm CC'. Tính góc giữa hai đường thẳng AD' và BM

Khối lăng trụ ABC.A'B'C' có đáy là tam giác đều, a là độ dài cạnh đáy. Góc giữa cạnh bên và đáy là ${30}^o$. Hình chiếu vuông góc của A' trên mặt (ABC) trùng với trung điểm của BC. Diện tích xung quanh của lăng trụ đã cho là

Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và $SA=a\sqrt{2}$. Thể tích V của khối chóp S.ABC là

Cho hình thang vuông ABCD có $\hat{A}=\hat{D}={90}^o$, AB=AD=2cm, CD=2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA - 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD'  là $\frac{9\pi }{2}{a}^3$.

Tính thể tích V của hình chữ nhật 

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khối nón đỉnh A, đáy là đường tròn đi qua ba điểm A'BD có thể tích bằng

Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích V. Gọi M là trung điểm của CC'. Mặt phẳng (MAB) chia khối trụ thành hai phần. Tính tỷ số thể tích hai phần đó (số bé chia số lớn)

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , BC = $a\sqrt{3}$ , SA = a và SA vuông góc với đáy ABCD. Tính sin $\alpha$ với $\alpha$ là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC)

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và SB = 2a. Góc giữa đường thẳng SB và mặt phẳng đáy bằng

Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, AB = a, SA vuông góc với mặt phẳng đáy và SA = 2a . Khoảng cách từ A đến mặt phẳng (SBC) bằng

Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích của khối chóp đã cho bằng

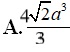
Cho khối cầu (S) ngoại tiếp tứ diện OABC có OA = OB = OC = a và OA, OB, OC đôi một vuông góc. Thể tích của (S) bằng

Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng 2a. Thể tích của khối lăng trụ đã cho bằng

Cho lăng trụ ABC.A’B’C’ có khoảng cách từ điểm A đến mặt phẳng (A’BC) bằng 6a. Khoảng cách từ trung điểm M cạnh B’C’ đến mặt phẳng (A’BC) bằng

Cho khối chóp S.ABCD có đáy là hình bình hành, thể tích bằng 1. Gọi M là trung điểm cạnh SA; các điểm E,F lần lượt là điểm đối xứng của A qua B và D. Mặt phẳng (MEF) cắt các cạnh SB,SD lần lượt tại các điểm N,P. Thể tích của khối đa diện ABCDMNP bằng

Thể tích khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = 3a (tham khảo hình vẽ bên) bằng

Cho khối chóp S.ABCD có đáy là hình thang với hai đáy là AB và CD, AB = 2CD. Gọi E là một điểm trên cạnh SC. Mặt phẳng (ABE) chia khối chóp S.ABCD thành hai khối đa diện có thể tích bằng nhau. Tính tỉ số $\frac{SE}{SC}$ 

Cho khối hộp đứng có đáy là một hình thoi có độ dài đường chéo nhỏ bằng 10 và góc nhọn bằng  ${60}^o$ . Diện tích mỗi mặt bên của khối hộp bằng 10. Thể tích của khối hộp đã cho bằng

Cho hình lăng trụ đều có độ dài cạnh đáy bằng a. Chiều cao của hình lăng trụ bằng h, diện tích một mặt đáy bằng S. Tổng khoảng cách từ một điểm trong của hình lăng trụ đến tất cả các mặt của hình lăng trụ bằng