8 câu Trắc nghiệm Toán 10 chân trời sáng tạo Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ có đáp án (Phần 2) (Thông hiểu)
8 câu hỏi
Nga có điểm tổng kết 4 môn học như bảng sau:
Môn | Toán | Ngữ Văn | Tiếng Anh | Vật lí |
Điểm | 9,5 | 9,0 | 8,5 | 9,0 |
Điểm trung bình 4 môn học của Nga là bao nhiêu?
8,5;
8,75;
9,5;
9,0.
Một lớp học có 3 tổ học sinh, khi trồng cây trong buổi ngoại khóa có kết quả như sau:
Tổ | 1 | 2 | 3 |
Số học sinh | 9 | 10 | 9 |
Số cây | 27 | 31 | 25 |
Mỗi bạn học sinh đều không trồng quá 3 cây. Hỏi trong bảng đã thống kê sai tổ nào?
Tổ 1;
Tổ 2;
Tổ 3;
Cả 3 tổ.
Người ta thống kê ước tính tốc độ tăng kim ngạch xuất, nhập khẩu hàng hóa 2 tháng đầu năm giao đoạn 2018 – 2022 (%) như sau:
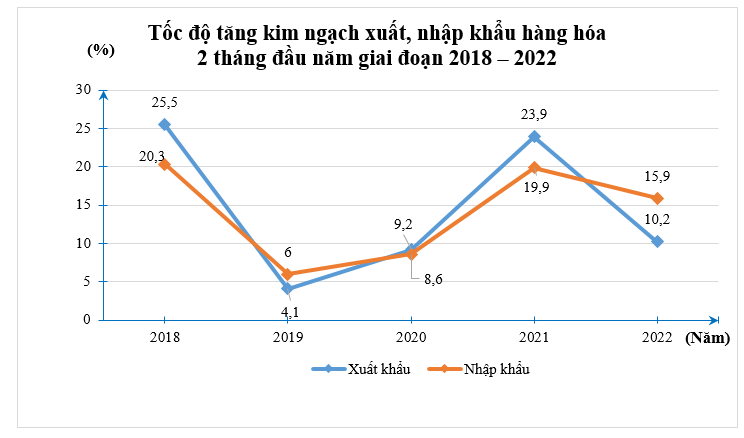
So với năm 2020 thì năm 2022 kim ngạch xuất khẩu tăng hay giảm bao nhiêu %?
Tăng 7,3%;
Giảm 1%;
Tăng 1%;
Tăng 5,1%;
Tổng số điểm 10 trong học kì II của lớp 10A là bao nhiêu?
200;
100;
125;
120.
Tổ nào có số điểm 10 ở học kì sau tiến bộ hơn học kì trước?
Tổ 1, 2;
Tổ 1, 2, 3;
Tổ 3, 4;
Cả 4 tổ.
Gọi x là tổng tỉ số của số điểm 10 của học kì II so với học kì I của cả 4 tổ. Tính x.
x = ;
x = ;
x = ;
x = .
Biểu đồ dưới đây thể hiện số lượng khách du lịch đến 3 tỉnh Hà Nội, Đà Nẵng và TP Hồ Chí Minh trong năm 2020 và năm 2021:
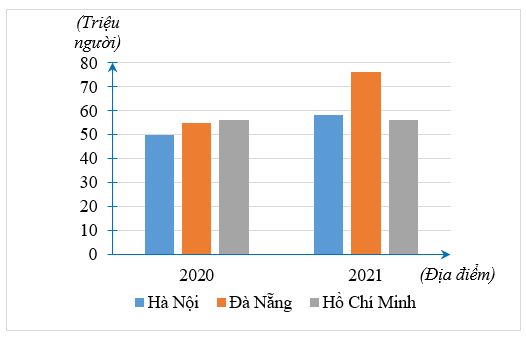
Hỏi bảng số liệu nào sau đây đúng với biểu đồ trên:
Năm
Địa điểm
2020
(triệu người)
2021
(triệu người)
Hà Nội
50
58
Đà Nẵng
55
76
Hồ Chí Minh
56
56
Năm
Địa điểm
2020
(triệu người)
2021
(triệu người)
Hà Nội
50
40
Đà Nẵng
55
76
Hồ Chí Minh
56
56
Năm
Địa điểm
2020
(triệu người)
2021
(triệu người)
Hà Nội
50
58
Đà Nẵng
76
21
Hồ Chí Minh
56
56
Năm
Địa điểm
2020
(triệu người)
2021
(triệu người)
Hà Nội
50
58
Đà Nẵng
55
76
Hồ Chí Minh
60
30
Trường THPT Amsterdam có số lượng học sinh khối 10 xếp loại sau học kì I như sau:
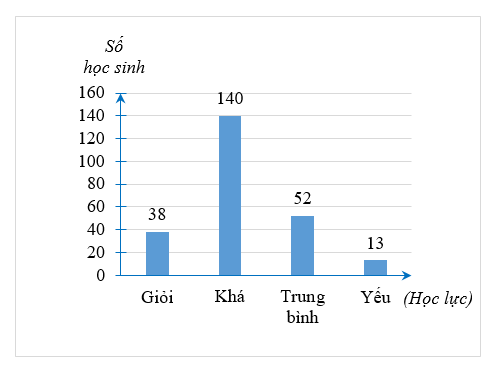
Biết số học sinh của khối 11 bằng 2 lần số học sinh khối 10. Hỏi số lượng học sinh khối 11 là bao nhiêu?
486;
502;
243;
438.