105 câu Trắc nghiệm Toán 11 Bài 2: Giới hạn dãy số có đáp án (Mới nhất)
105 câu hỏi
Chọn mệnh đề đúng trong các mệnh đề sau:
Nếu ![]() , thì
, thì ![]() .
.
Nếu ![]() , thì
, thì ![]() .
.
Nếu ![]() , thì
, thì ![]() .
.
Nếu ![]() , thì
, thì ![]() .
.
Giá trị của ![]() bằng:
bằng:
0
1
2
3
Giá trị của ![]()
![]() bằng:
bằng:
0
2
4
5
Giá trị của ![]() bằng:
bằng:
0
3
5
8
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
2
1
Giá trị của 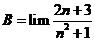 bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
1
Giá trị của ![]() bằng:
bằng:
- 3
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
0
4
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() với a > 0 bằng:
với a > 0 bằng:
0
1
Cho dãy số (un) với ![]() và
và ![]() . Chọn giá trị đúng của trong các số sau:
. Chọn giá trị đúng của trong các số sau:
.
.
0.
1.
Kết quả đúng của ![]() là:
là:
4.
5.
–4.
.
Giá trị của bằng:
1
Giá trị của ![]() bằng:
bằng:
1
Kết quả đúng của ![]() là
là
.
.
.
.
Giới hạn dãy số (un) với ![]() là:
là:
.
.
.
0.
Chọn kết quả đúng của ![]() :
:
5.
.
-.
.
Giá trị của 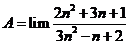 bằng:
bằng:
1
Giá trị của 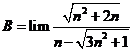 bằng:
bằng:
0
Giá trị của 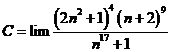 bằng:
bằng:
16
1
Giá trị của 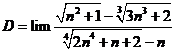 bằng:
bằng:
1
Giá trị của 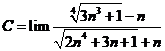 bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
8
1
Giá trị của ![]() bằng:
bằng:
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của bằng:
0
1
Giá trị của 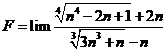 bằng:
bằng:
1
Cho dãy số un với ![]() . Chọn kết quả đúng của là:
. Chọn kết quả đúng của là:
.
0.
1.
.
![]() bằng:
bằng:
10
0
Tính giới hạn: ![]()
1.
0.
-1
.
Tính giới hạn: ![]()
0.
.
.
1.
Chọn kết quả đúng của ![]() .
.
4.
3.
2.
.
Giá trị của ![]() (Trong đó k; p là các số nguyên dương;
(Trong đó k; p là các số nguyên dương; ![]() ) bằng:
) bằng:
Đáp án khác
1
Kết quả đúng của ![]() là:
là:
.
.
.
.
![]() bằng:
bằng:
.
.
0.
1.
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị đúng của Lim (3n - 5n) là:
.
.
2.
-2.
Giá trị của. ![]() bằng:
bằng:
2
1
![]() bằng:
bằng:
.
0.
1
.
![]() bằng :
bằng :
.
.
.
Giá trị của. ![]() bằng:
bằng:
0
1
Cho các số thực a,b thỏa ![]() . Tìm giới hạn
. Tìm giới hạn ![]() .
.
1
Tính giới hạn của dãy số ![]() với
với ![]()
Đáp án khác
1
![]() bằng:
bằng:
.
0.
.
.
Giá trị của. ![]() bằng:
bằng:
3
1
Giá trị của ![]() bằng:
bằng:
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
1
Giá trị đúng của là:
.
.
0.
1.
Giá trị của ![]() bằng:
bằng:
3
1
Giá trị của ![]() bằng:
bằng:
0
3
Giá trị của ![]() bằng:
bằng:
1
Giá trị của. ![]() bằng:
bằng:
0
1
Giá trị của. ![]() bằng:
bằng:
1
Giá trị của. ![]() bằng:
bằng:
0
1
Giá trị đúng của ![]() là:
là:
- 1.
0.
1.
.
Giá trị của. ![]() bằng:
bằng:
1
Giá trị của ![]() bằng:
bằng:
2
D.
![]() bằng :
bằng :
.
.
2.
1.
Giá trị của. ![]() bằng:
bằng:
2
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
0
1
Giá trị của ![]() bằng:
bằng:
Đáp án khác
1
Tính giới hạn của dãy số ![]() :
:
0
1
Tính giới hạn của dãy số ![]() :
:
1
Tính giới hạn của dãy số ![]() trong đó
trong đó ![]() :
:
1
Tính giới hạn của dãy số ![]() :
:
1
Tính giới hạn của dãy số ![]() :
:
3
1
Tính giới hạn của dãy số ![]() với
với 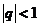
Tính giới hạn của dãy số ![]() :
:
3
1
Tính giới hạn của dãy số ![]()
3
Tính giới hạn của dãy số ![]()
3
Tính giới hạn của dãy số ![]()
1
Cho dãy số (xn) xác định bởi ![]()
Đặt ![]() . Tính Sn.
. Tính Sn.
2
1
Cho dãy (xk) được xác định như sau: ![]()
Tìm un với ![]() .
.
Cho dãy số (xn) được xác định bởi: 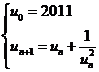 . Tìm
. Tìm ![]() .
.
3
1
Cho dãy x > 0 xác định như sau: ![]() . Tìm .
. Tìm .
2010
1
Tìm lim un biết ![]()
1
Tìm lim un biết 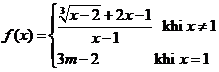
2
Tìm lim un biết 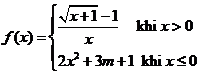
2
1
Tìm lim un biết 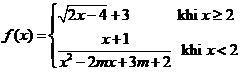 trong đó .
trong đó .
1
Tìm lim un biết ![]()
3
1
Tìm lim un biết 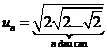
2
1
Gọi ![]() là dãy số xác định bởi
là dãy số xác định bởi ![]() . Tìm
. Tìm ![]() .
.
1
Cho dãy số ![]() được xác định như sau
được xác định như sau ![]() .
.
Đặt ![]() . Tìm
. Tìm ![]() .
.
1
Cho 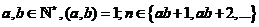 . Kí hiệu rn là số cặp số
. Kí hiệu rn là số cặp số ![]() sao cho
sao cho ![]() . Tìm .
. Tìm .![]()
ab - 1
Cho dãy số có giới hạn (un) xác định bởi: 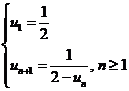 . Tìm kết quả đúng của lim un .
. Tìm kết quả đúng của lim un .
0.
1.
-1.
Tìm giá trị đúng của ![]() .
.
.
2.
.
.
Tính giới hạn: 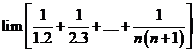
0
1.
.
Không có giới hạn.
Tính giới hạn: 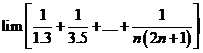
1.
0.
.
2.
Tính giới hạn: 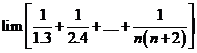
.
0.
1.
.
Tính giới hạn: ![]() .
.
.
2.
1.
.
Tính giới hạn: ![]() .
.
1.
.
.
.




