14 câu hỏi
Cho hàm số f(x) = 2x3 + ax2 + bx + c có f(0) = 2f'(0) và f(x) ≥ 2f'(x) với mọi x ≥ ‒1. Có bao nhiêu giá tị nguyên của a để hàm số f(x) đồng biến trên ℝ?
Vô số.
11.
1.
10.
Cho hình lăng trụ tam giác đều. Trong các mệnh đề sau mệnh đề nào là sai?
Hai đáy là các tam giác đều bằng nhau.
Các mặt bên là hình vuông.
Các cạnh bên vuông góc với mặt đáy.
Các cạnh bên bằng nhau.
Cho parabol (P): y = x2 ‒ 2x + 5 và đường thẳng d: y = 2mx + 2 ‒ 3m. Tìm tất cả các giá trị m để (P) cắt d tại hai điểm phân biệt nằm phía bên phải trục tung?
\[1 < m < \frac{7}{3}.\]
m > 1.
\[m > \frac{7}{3}.\]
m < 1.
Cho tam giác ABC cân tại A có \[\widehat A = 120^\circ \] nội tiếp đường tròn (O; 3 cm). Khi đó diện tích tam giác ABC là
\[\frac{{9\sqrt 3 }}{4}\] cm2.
\[\frac{{3\sqrt 3 }}{2}\] cm2.
\[3\sqrt 3 \] cm2.
\[\frac{{3\sqrt 3 }}{4}\] cm2.
Có bao nhiêu số palindrom gồm 5 chữ số (Số palindrom là số mà nếu ta viết các chữ số theo thứ tự ngược lại thì giá trị của nó không thay đổi):
900.
10 000.
810.
729.
Có 6 bạn nam trong đó có Hoàng và 3 bạn nữ xếp ngẫu nhiên thành một hàng ngang. Xác xuất để không có hai bạn nữ nào đứng cạnh nhau và Hoàng đứng ở ngoài cùng bằng
\[\frac{{10}}{{21}}.\]
\[\frac{5}{{126}}.\]
\[\frac{5}{{21}}.\]
\[\frac{5}{{63}}.\]
Diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số y = x2 ‒ 2x và y = x là
\[S = \frac{9}{4}.\]
\[S = \frac{9}{2}.\]
\[S = \frac{{13}}{2}.\]
\[S = \frac{{13}}{4}.\]
Diện tích của năm tỉnh Kon Tum, Gia Lai, Đăk Lăk, Đăk Nông và Lâm Đồng được thống kê ở bảng sau:
|
Tỉnh |
Kon Tum |
Gia Lai |
Đăk Lăk |
Đăk Nông |
Lâm Đồng |
|
Diện tích (km2) |
9 674 |
15 510 |
13 030 |
6 509 |
9 783 |
Tổng diện tích năm tỉnh Kon Tum, Gia Lai, Đăk Lăk, Đăk Nông và Lâm Đồng bằng bao nhiêu phần trăm diện tích miền Nam Việt Nam (làm tròn kết quả đến hàng đơn vị), biết diện tích miền Nam Việt Nam là 77 700 km2)?
70%.
71%.
69%.
61%.
Cho các hàm số y = logax và y = logbx có đồ thị như hình vẽ
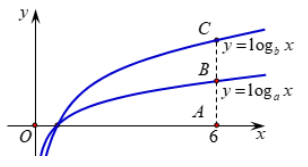
Đường thẳng x = 6 cắt trục hoành, đồ thị hàm số y = logax và y = logbx lần lượt tại A, B và C. Nếu \[\frac{{AC}}{{AB}} = {\log _2}3\] thì khẳng định nào sau đây là đúng?
b2 = a3.
b3 = a2.
log2b = log3a.
log3b = log2a.
Hành lang trong một tòa nhà có dạng chữ L (hình vẽ) có chiều cao 2 m, một phía rộng 1m, một phía rộng 1, 2 m. Một người thợ cần mang một số ống thép cứng các loại có độ dài 2 m, 2, 5 m, 3 m, 3,5 m, 4 m, từ bên này qua bên kia. Hỏi có thể mang được mấy loại qua lối đi đó?
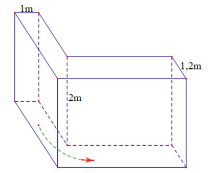
4 loại.
3 loại.
5 loại.
2 loại.
Cho hàm số \[y = 2x - 1 + \frac{3}{{x + 3}}\left( C \right).\] Khoảng cách từ điểm M(2; ‒1) đến tiệm cận xiên của đồ thị (C) là
\[\frac{2}{{\sqrt 5 }}.\]
\[\frac{4}{{\sqrt 5 }}.\]
2.
4.
Làm tròn số 25,0769 đến hàng phần trăm ta được kết quả là:
25,08.
25,07.
25,06.
25,09.
Tìm tập nghiệm S của phương trình \[{\log _{\sqrt 2 }}x + {\log _{\frac{1}{2}}}\left( {2x - 1} \right) = 2\] có dạng \[x = a + b\sqrt 3 \] (a, b là hai số nguyên). Giá trị của a + b bằng
6.
4.
10.
2.
Trong không gian Oxyz, cho hai điểm A(1; 2; ‒2), B(2; ‒1; 2). Tìm tọa độ điểm M trên mặt phẳng Oxy sao cho MA + MB đạt giá trị nhỏ nhất.
M(1; 1; 0).
\[M\left( {\frac{3}{2};\,\,\frac{1}{2};\,\,0} \right).\]
M(2; 1; 0).
\[M\left( {\frac{1}{2};\,\,\frac{3}{2};\,\,0} \right).\]
