10 câu hỏi
Cho hai biến cố A, B với P(B) = 0,6; P(A|B) = 0,7 và \(P\left( {A|\overline B } \right) = 0,4\). Khi đó P(A) bằng
0,7;
0,4;
0,58;
0,52.
Cho hai biến cố A và B biết P(A|B) = 0,08; \(P\left( {\overline A |\overline B } \right) = 0,63\); P(B) = 0,03. Khi đó xác suất xảy ra biến cố A là bao nhiêu?
0,112;
0,5231;
0,3613;
0,063.
Cho A, B là hai biến cố. Biết P(B) = 0,2. Nếu B không xảy ra thì tỉ lệ A xảy ra là 2%. Nếu B xảy ra thì tỉ lệ A xảy ra 4%. Xác suất của biến cố A là bao nhiêu?
0,018;
0,036;
0,028;
0,024.
Có hai hộp đựng các viên bi. Hộp thứ nhất đựng 5 bi đỏ và 3 bi vàng, hộp thứ hai đựng 4 bi đỏ và 2 bi vàng. Lấy ngẫu nhiên một bi từ hộp thứ nhất bỏ sang hộp thứ hai, sau đó lấy ngẫu nhiên một bi từ hộp thứ hai. Xác suất để bi lấy ra từ hộp thứ hai là bi đỏ thuộc khoảng nào sau đây?
(0,65; 0,67);
(0,57; 0,59);
(0,61; 0,63);
(0,63; 0,65).
Một lớp học có số lượng học sinh nam chiếm 65%. Tỉ lệ học sinh nam học khá môn Tiếng Anh là 75%, tỉ lệ học sinh nữ học khá môn Tiếng Anh là 82%. Nếu ta gặp ngẫu nhiên một bạn học sinh trong lớp thì xác suất để bạn học sinh này học khá môn Tiếng Anh thuộc khoảng nào sau đây.
(0,7; 0,75);
(0,65; 0,7);
(0,75; 0,8);
(0,8; 0,85).
Hai máy tự động sản xuất cùng một loại chi tiết, trong đó máy I sản xuất 35%, máy II sản xuất 65% tổng sản lượng. Tỉ lệ phế phẩm của các máy lần lượt là 0,3% và 0,7%. Chọn ngẫu nhiên 1 sản phẩm từ kho. Tính xác suất để chọn được phế phẩm.
0,0056;
0,0065;
0,065;
0,056.
Có 2 xạ thủ loại I và 8 xạ thủ loại II, xác suất bắn trúng đích của các loại xạ thủ loại I là 0,9 và loại II là 0,7. Chọn ngẫu nhiên ra một xạ thủ và xạ thủ đó bắn một viên đạn. Tìm xác suất để viên đạn đó trúng đích.
0,74;
0,86;
0,56;
0,68.
Một hộp bút bi Thiên Long có 15 chiếc bút trong đó có 9 chiếc bút mới. Người ta lấy ngẫu nhiên 1 chiếc bút để sử dụng sau đó trả lại vào hộp. Lần thứ hai lấy ngẫu nhiên 2 chiếc bút, tính xác suất cả hai chiếc bút lấy ra đều là chiếc mới.
\(\frac{{52}}{{175}}\);
\(\frac{{52}}{{177}}\);
\(\frac{{53}}{{175}}\);
\(\frac{{25}}{{175}}\).
Giả sử tỉ lệ người dân của tỉnh Khánh Hòa nghiện thuốc lá là 20%, tỉ lệ người bị bệnh phổi trong số người nghiện thuốc là là 70%, trong số người không nghiện thuốc là là 15%. Hỏi khi ta gặp ngẫu nhiên một người dân của tỉnh Khánh Hòa thì khả năng mà người đó bị bệnh phổi là
15%;
29%;
31%;
26%.
Cho sơ đồ hình cây như hình bên.
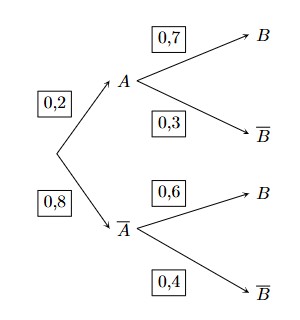
Xác suất của biến cố B là
0,42;
0,62;
0,28;
0,48.
